Question

【题目】已知函数f（x）为二次函数，且f（x﹣1）+f（x）=2x2+4．
（1）求f（x）的解析式；
（2）当x∈[t，t+2]，t∈R时，求函数f（x）的最小值（用t表示）．

Answer 1

【答案】
（1）解：设f（x）=ax2+bx+c，

∴

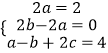
解得∴

∴f（x）=x2+x+2

（2）解：∵f（x）=x2+x+2的对称轴为 ；

当 即 时 ；

当 时，f（x）=x2+x+2在x∈[t，t+2]上单调递增， ；

当 时，f（x）=x2+x+2在x∈[t，t+2]上单调递减， ；

综上：f（x）min=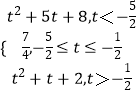

【解析】（1）首先设出函数的解析式，利用待定系数法即可；（2）判断函数f（x）的对称轴与区间[t，t+2]的位置关系，再根据图形特征求出最小值；
【考点精析】根据题目的已知条件，利用二次函数的性质的相关知识可以得到问题的答案，需要掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减．