题目内容
已知符号函数sgn(x)=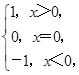 则函数f(x)=sgn(ln x)-ln2x的零点个数为 ( ).
则函数f(x)=sgn(ln x)-ln2x的零点个数为 ( ).
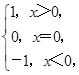 则函数f(x)=sgn(ln x)-ln2x的零点个数为 ( ).
则函数f(x)=sgn(ln x)-ln2x的零点个数为 ( ). | A.1 | B.2 | C.3 | D.4 |
B
当x>1时,ln x>0,sgn(ln x)=1,
∴f(x)=1-ln2x,令f(x)=0,得x=e.
当x=1时,ln x=0,sgn(ln x)=0,
∴f(x)=-ln2x,令f(x)=0,得x=1满足.
当0<x<1时,ln x<0,sgn(ln x)=-1,
∴f(x)=-1-ln2x<0,f(x)=0无解.
∴函数f(x)的零点为x=1与x=e.
∴f(x)=1-ln2x,令f(x)=0,得x=e.
当x=1时,ln x=0,sgn(ln x)=0,
∴f(x)=-ln2x,令f(x)=0,得x=1满足.
当0<x<1时,ln x<0,sgn(ln x)=-1,
∴f(x)=-1-ln2x<0,f(x)=0无解.
∴函数f(x)的零点为x=1与x=e.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 (
(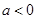 ).
).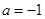 ,求函数
,求函数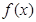 的极值;
的极值;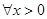 ,不等式
,不等式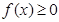 恒成立,求实数
恒成立,求实数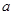 的取值范围.
的取值范围.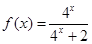
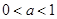 ,求
,求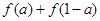 的值;
的值;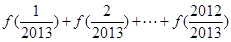 的值.
的值.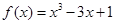 在区间
在区间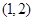 上的零点的近似值(精确度
上的零点的近似值(精确度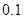 )是 .
)是 . 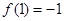





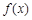 的定义域为R,若存在常数
的定义域为R,若存在常数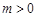 ,对任意
,对任意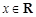 ,有
,有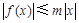 ,则称
,则称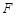 函数.给出下列函数:①
函数.给出下列函数:①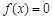 ; ②
; ②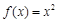 ; ③
; ③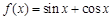 ;
;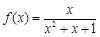 ; ⑤
; ⑤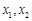 均
均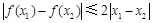 .其中是
.其中是