题目内容
10.已知f(x)=$\frac{1}{2}$ax2+ax+lnx,(1)当a=0时,g(x)=f(x)-(x-1)2.求g(x)在点(1,0)的切线方程;
(2)讨论f(x)的单调性.
分析 (1)求导数,确定切线的斜率,可得g(x)在点(1,0)的切线方程;
(2)利用导数的正负,讨论f(x)的单调性.
解答 解:(1)当a=0时,g(x)=f(x)-(x-1)2=lnx-(x-1)2.
∴g′(x)=$\frac{1}{x}$-2x+2,
∴g′(1)=1,
∴g(x)在点(1,0)的切线方程为y-0=x-1,即x-y-1=0;
(2)∵f(x)=$\frac{1}{2}$ax2+ax+lnx,
∴f′(x)=ax+a+$\frac{1}{x}$=$\frac{a{x}^{2}+ax+1}{x}$,
∴若a≥0,f′(x)≥0,函数在(0,+∞)上单调递增;
a<0,f′(x)<0,函数在(0,$\frac{-a+\sqrt{{a}^{2}-4a}}{2a}$)上单调递增,在($\frac{-a+\sqrt{{a}^{2}-4a}}{2a}$,+∞)上单调递减.
点评 本题考查导数的综合运用,考查导数的几何意义,单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.(1+$\frac{1}{2}$x)5的展开式中的第三项的系数为( )
| A. | 5 | B. | $\frac{5}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{8}$ |
15.如图所示,四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得到AB∥面MNP的图形的序号是( )
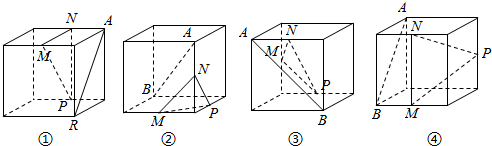

| A. | ①② | B. | ②④ | C. | ①③ | D. | ①④ |

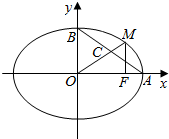 如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.
如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.