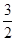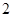题目内容
(本题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD为直角梯形,AD∥BC, BAD=90°,PA
BAD=90°,PA 底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.

(Ⅰ)求证:PB 平面ADMN;
平面ADMN;
(Ⅱ)求四棱锥P-ADMN的体积.
如图,在四棱锥P—ABCD中,底面ABCD为直角梯形,AD∥BC,
 BAD=90°,PA
BAD=90°,PA 底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
(Ⅰ)求证:PB
 平面ADMN;
平面ADMN;(Ⅱ)求四棱锥P-ADMN的体积.
(I)利用线面垂直得AD^平面PAB,
∴AD^PB.根据等腰三角形得AN^PB.推出PB^平面ADMN.
(II)V=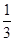 S×PN=
S×PN=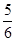 .
.
∴AD^PB.根据等腰三角形得AN^PB.推出PB^平面ADMN.
(II)V=
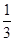 S×PN=
S×PN=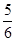 .
. 试题分析:(I)∵PA^底面ABCD,ÐBAD=90°,AB∩AD=D,∴AD^平面PAB,
又PBÌ平面PAB,∴AD^PB.……3分
∵PA=AB,∴DPAB为等腰直角三角形,N为PB的中点,∴AN^PB.
∵AN∩AD=D,∴PB^平面ADMN.……6分
(II)由(Ⅰ)PB^平面ADMN,
∴PN为四棱锥P-ADMN的高,且PN=
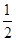 PB=
PB=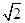 .……8分
.……8分四边形ADMN为直角梯形,且MN
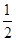 BC,∴MN=
BC,∴MN=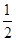 ,AN=
,AN=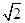 ,
,∴四边形ADMN的面积为S=
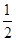 (2+
(2+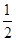 )×
)×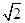 =
=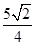 ,……11分
,……11分∴四棱锥P-ADMN的体积V=
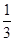 S×PN=
S×PN=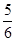 . ……12分
. ……12分点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤。本题通过空间直角坐标系,利用向量知识可简化证明过程。把证明问题转化成向量的坐标运算,这种方法带有方向性。

练习册系列答案
相关题目

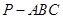 中,
中, 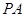 、
、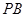 、
、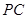 两两垂直, 且
两两垂直, 且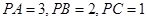 .设
.设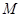 是底面
是底面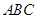 内一点,定义
内一点,定义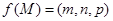 ,其中
,其中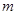 、
、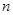 、
、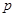 分别是三棱锥M-PAB、 三棱锥M-PBC、三棱锥M-PCA的体积.若
分别是三棱锥M-PAB、 三棱锥M-PBC、三棱锥M-PCA的体积.若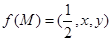 ,且
,且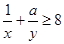 恒成立,则正实数
恒成立,则正实数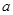 的最小值为___ ___.
的最小值为___ ___.

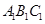 中,
中,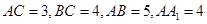 ,点
,点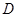 是
是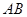 的中点.
的中点. 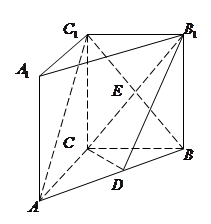
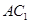 ∥平面
∥平面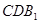 ;
;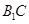 所成的角的余弦值;
所成的角的余弦值;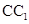 与平面
与平面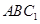 所成角的正弦值;
所成角的正弦值;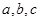 是三条不同的直线,
是三条不同的直线,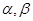 是两个不同的平面,在下列命题:
是两个不同的平面,在下列命题: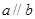 ,且
,且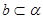 ,则
,则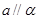
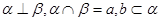 ,且
,且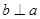 ,则
,则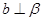
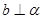 ,则
,则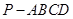 中,
中,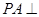 底面
底面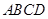 ,
,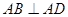 ,
,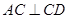 ,
,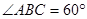 ,
,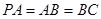 ,
,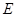 是
是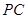 的中点。
的中点。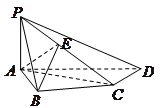
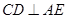 ;
;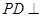 平面
平面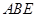 ;
;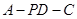 的正切值.
的正切值.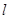 和平面
和平面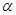 内的一条直线平行,那么直线
内的一条直线平行,那么直线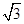 ,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为
,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为 
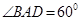 且边长是2的菱形
且边长是2的菱形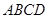 ,沿它的对角线
,沿它的对角线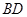 折成60°的二面角,则( )
折成60°的二面角,则( )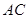 与
与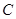 到平面
到平面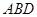 的距离是 .
的距离是 .