题目内容
如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2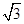 ,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为
,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为 
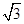 ,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为
,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为 
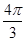 。
。试题分析:因为∠BAD=90°,所以AD⊥AB,又AD⊥BC,且AB
 BC=B,所以AD⊥平面ABC。
BC=B,所以AD⊥平面ABC。在平面ABC内,取点P,连PA,则
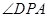 是DP与平面ABC所成角。
是DP与平面ABC所成角。又因为AD=4,所以直线DP与平面ABC所成角的正切值为2,须AP=2,即点P在△ABC内所成的轨迹是以A为圆心,半径为2 的圆的一部分。
而∠BAC=120°=
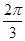 ,故点P在△ABC内所成的轨迹的长度为
,故点P在△ABC内所成的轨迹的长度为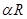 =
=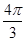 。
。点评:典型题,综合性较强,考查知识全面,可谓之是“证算并重题”,较好地考查了数形结合思想及学生的逻辑推理能力、计算能力。解答本题的关键是认识到“点P在△ABC内所成的轨迹是以A为圆心,半径为2 的圆的一部分。”

练习册系列答案
相关题目
 的底面边长为4,高为3,在正三棱锥内任取一点
的底面边长为4,高为3,在正三棱锥内任取一点 ,使得
,使得 的概率是( )
的概率是( )



 BAD=90°,PA
BAD=90°,PA 底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
 中,已知 PA⊥平面ABCD,
中,已知 PA⊥平面ABCD, 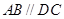 ,
, 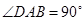 ,
,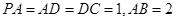 ,
,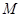 为
为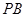 的中点.
的中点.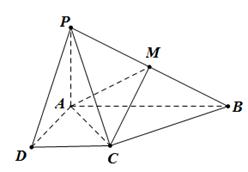
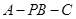 的平面角的正切值.
的平面角的正切值.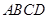 中,
中,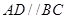 ,
,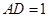 ,
,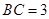 ,
,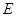 为
为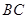 上一点,
上一点, 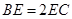 ,且
,且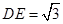 .将梯形
.将梯形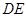 折成直二面角
折成直二面角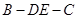 ,如图2所示.
,如图2所示.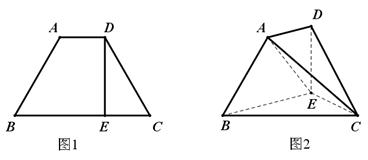
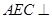 平面
平面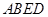 ;
;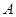 关于点
关于点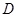 的对称点为
的对称点为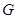 ,点
,点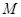 在
在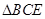 所在平面内,且直线
所在平面内,且直线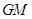 与平面
与平面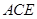 所成的角为
所成的角为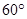 ,试求出点
,试求出点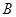 的最短距离.
的最短距离.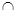 β=m,n与α、β所成的角相等,则m⊥n
β=m,n与α、β所成的角相等,则m⊥n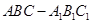 中,侧棱
中,侧棱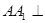 底面
底面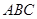 ,
,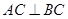 ,
,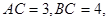
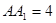 ,
,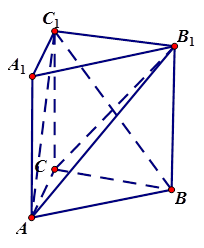
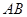 与
与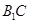 所成角的余弦值;
所成角的余弦值;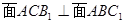
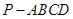 中,
中,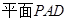
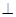 平面
平面 ,底面
,底面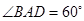 .
.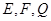 分别是
分别是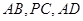 的中点.
的中点.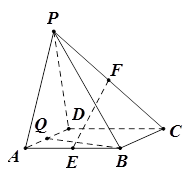
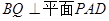 ;
;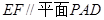 .
.