题目内容
(本题15分)如图,在四棱锥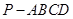 中,
中,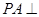 底面
底面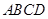 ,
,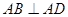 ,
,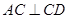 ,
,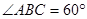 ,
,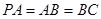 ,
,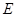 是
是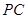 的中点。
的中点。
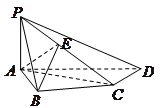
(Ⅰ)证明: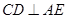 ;
;
(Ⅱ)证明: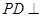 平面
平面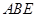 ;
;
(Ⅲ)求二面角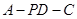 的正切值.
的正切值.
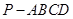 中,
中,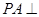 底面
底面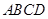 ,
,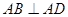 ,
,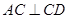 ,
,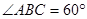 ,
,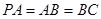 ,
,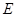 是
是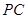 的中点。
的中点。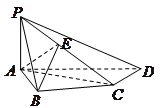
(Ⅰ)证明:
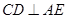 ;
;(Ⅱ)证明:
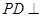 平面
平面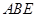 ;
;(Ⅲ)求二面角
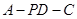 的正切值.
的正切值.(1)四棱锥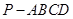 中,因
中,因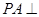 底面
底面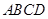 ,故
,故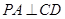 ,结合
,结合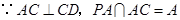 ,
,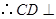 平面
平面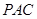 ,进而证明
,进而证明
(2)根据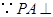 底面
底面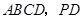 在底面
在底面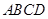 内的射影是
内的射影是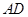 ,
,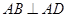 ,
,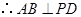 ,从而证明。
,从而证明。
(3)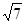
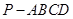 中,因
中,因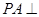 底面
底面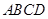 ,故
,故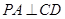 ,结合
,结合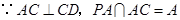 ,
,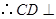 平面
平面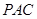 ,进而证明
,进而证明(2)根据
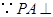 底面
底面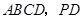 在底面
在底面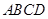 内的射影是
内的射影是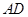 ,
,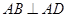 ,
,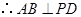 ,从而证明。
,从而证明。(3)
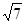
试题分析:解法一:
(Ⅰ)证明:在四棱锥
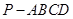 中,因
中,因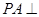 底面
底面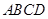 ,
,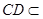 平面
平面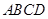 ,
,故
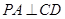 .
.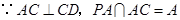 ,
,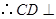 平面
平面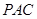 .
.而
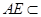 平面
平面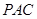 ,
,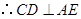 .…………………4分
.…………………4分(Ⅱ)证明:由
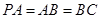 ,
,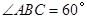 ,可得
,可得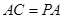 .
.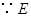 是
是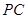 的中点,
的中点,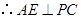 .
.由(Ⅰ)知,
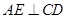 ,且
,且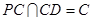 ,所以
,所以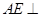 平面
平面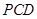 .
.而
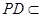 平面
平面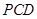 ,
,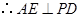 .
.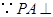 底面
底面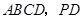 在底面
在底面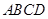 内的射影是
内的射影是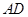 ,
,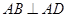 ,
,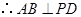 .
.又
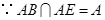 ,综上得
,综上得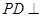 平面
平面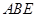 . …………………9分
. …………………9分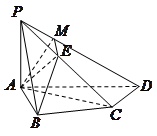
(Ⅲ)过点
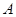 作
作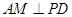 ,垂足为
,垂足为 ,连结
,连结 .则(Ⅱ)知,
.则(Ⅱ)知,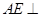 平面
平面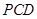 ,
,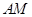 在平面
在平面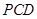 内的射影是
内的射影是 ,则
,则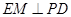 .
.因此
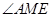 是二面角
是二面角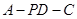 的平面角.
的平面角.由已知,得
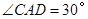 .设
.设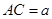 ,
,可得
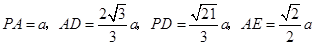 .
.在
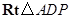 中,
中,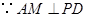 ,
,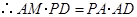 ,
,则
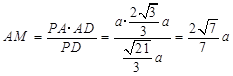 .
.在
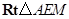 中,
中,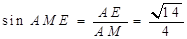 .
.所以二面角
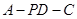 的正切值为
的正切值为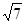 . ………………15分
. ………………15分解法二:
(Ⅰ)证明:以AB、AD、AP为x、y,z轴建立空间直角坐标系,设AB=a.
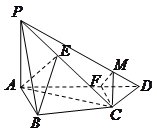
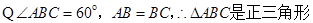
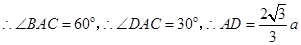
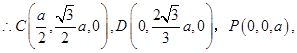
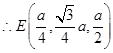
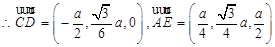
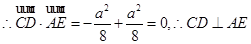 …………………5分
…………………5分(Ⅱ)证明:
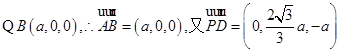
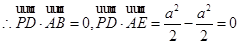
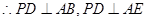
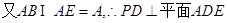 …………………9分
…………………9分(Ⅲ)设平面PDC的法向量为
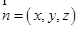
则
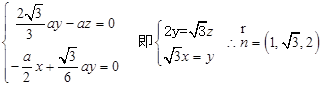
又平面APD的法向量是
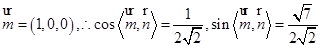
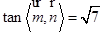 ,所以二面角
,所以二面角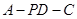 的正切值是
的正切值是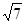 …………………15分
…………………15分点评:解决该试题的关键是利用空间中的点线面的位置关系,来结合定理加以证明,同时结合向量法求解二面角,需要运算细心点,中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 、
、 为两条不同的直线,
为两条不同的直线, 、
、 为两个不同的平面,则下列推理中正确的是( )
为两个不同的平面,则下列推理中正确的是( )




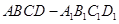 中,
中, ,点
,点 为
为 的中点,点
的中点,点 在
在 上,若
上,若 平面
平面 ,则
,则 ________.
________.
 中,E为AC中点
中,E为AC中点

 ,
, BAD=90°,PA
BAD=90°,PA 底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
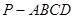 中,四边形
中,四边形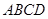 为正方形,
为正方形,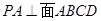 ,且
,且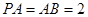 ,
,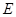 为
为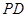 中点.
中点.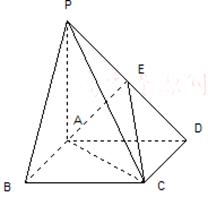
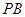 //平面
//平面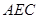 ;
;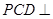 平面
平面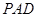 ;
;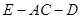 的正弦值.
的正弦值.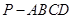 中,已知 PA⊥平面ABCD,
中,已知 PA⊥平面ABCD, 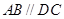 ,
, 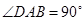 ,
,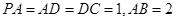 ,
,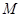 为
为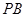 的中点.
的中点.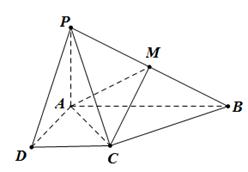
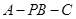 的平面角的正切值.
的平面角的正切值.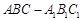 中,
中,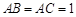 ,
,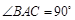 ,且异面直线
,且异面直线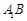 与
与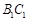 所成的角等于
所成的角等于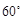 .
.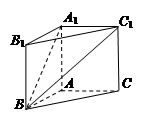
 所成的角的大小.
所成的角的大小.