题目内容
15.双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的焦点坐标为( )| A. | (±$\sqrt{7}$,0) | B. | (0,±$\sqrt{7}$) | C. | (±5,0) | D. | (0,±5) |
分析 求得双曲线的a,b,由c=$\sqrt{{a}^{2}+{b}^{2}}$,结合焦点在y轴上,即可得到所求焦点坐标.
解答 解:双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的a=3,b=4,
c=$\sqrt{{a}^{2}+{b}^{2}}$=5,
即有焦点坐标为(0,±5).
故选:D.
点评 本题考查双曲线的方程和性质,主要考查焦点的求法,属于基础题.

练习册系列答案
相关题目
15.已知x∈R,m=(x+1)(x2+$\frac{x}{2}$+1),n=(x+$\frac{1}{2}$)(x2+x+1),则m,n的大小关系为( )
| A. | m=n | B. | m>n | C. | m≤n | D. | m<n |
3.下列推理中属于类比推理的是( )
| A. | 一切偶数都能被2整除,2100是偶数,所以2100能被2整除. | |
| B. | 由a1,a2,a3…,归纳出数列的通项公式an | |
| C. | 由平面三角形的性质,推测空间四边形的性质 | |
| D. | 如果a>b,c>d,则a-d>b-c |
7.如图所示的程序框图,输出的S的值为( )
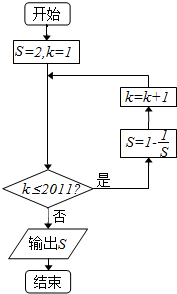

| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | -$\frac{1}{2}$ |
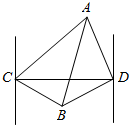 如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).
如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).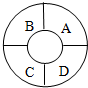 有4种不同的备选颜色给如图示的A、B、C、D四块涂色,要求每块涂同一种颜色,且相邻两块涂不同的颜色,则不同的涂色方法有( )种.
有4种不同的备选颜色给如图示的A、B、C、D四块涂色,要求每块涂同一种颜色,且相邻两块涂不同的颜色,则不同的涂色方法有( )种.
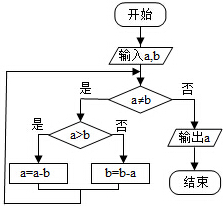 如图,该程序框图的算法思路源于我国古代数学专著《九章算术》中的“更相减损术”,执行此程序框图,若输入的m,n分别为72,168,则输出的m=( )
如图,该程序框图的算法思路源于我国古代数学专著《九章算术》中的“更相减损术”,执行此程序框图,若输入的m,n分别为72,168,则输出的m=( )