下列推理中属于类比推理的是( )A．一切偶数都能被2整除.2100是偶数.所以2100能被2整除．B．由a1.a2.a3-.归纳出数列的通项公式anC．由平面三角形的性质.推测空间四边形的性质D．如果a＞b.c＞d.则a-d＞b-c 题目和参考答案——青夏教育精英家教网——

题目内容

3．下列推理中属于类比推理的是（　　）

	A．	一切偶数都能被2整除，2¹⁰⁰是偶数，所以2¹⁰⁰能被2整除．
	B．	由a₁，a₂，a₃…，归纳出数列的通项公式a_n
	C．	由平面三角形的性质，推测空间四边形的性质
	D．	如果a＞b，c＞d，则a-d＞b-c

分析利用归纳推理、类比推理和演绎推理的定义进行判断，即可得出结论．

解答解：A，一切偶数都能被2整除，.2¹⁰⁰是偶数，所以2¹⁰⁰能被2整除，为演绎推理；
B，由a₁，a₂，a₃…，归纳出数列的通项公式a_n，是归纳推理；
C，由平面三角形的性质，推测空间四面体的性质，为类比推理；
D，如果a＞b，c＞d，则a-d＞b-c，为演绎推理．
故选：C．

点评本题考查的知识点是类比推理，熟练掌握归纳推理、类比推理和演绎推理的定义，是解答本题的关键．

练习册系列答案

贵州中考系列答案

滚动迁移中考总复习系列答案

海东青中考ABC卷系列答案

好学生课时检测系列答案

好学生口算计算应用一卡通系列答案

毕业生升学文化课考试说明系列答案

各地期末卷真题汇编系列答案

毕业生学业考试说明与检测系列答案

河南中考全程总复习系列答案

最新中考信息卷系列答案

相关题目

3．设y=$\frac{ln（3x+14）}{x}$，则y′|_x=-1=-（$\frac{3}{11}+ln11$）．

4．1.2log₆$\sqrt{2}$+3log₆$\root{3}{3}$=（　　）

log₆$\frac{2}{3}$

11．若一位学生把英语单词“error”中字母的拼写错了，则可能出现错误的种数是（　　）

如图所示是一个有n层（n≥2，n∈N^*）的六边形点阵，它的中心是一个点，算作第1层，第2层每边有2个点，第3层每边有3个点，…，第n层每边有n个点，则这个点阵共有（　　）个点．

8．函数f（x）在[a，b]上有定义，若对任意x₁，x₂∈[a，b]，有$f（\frac{{{x_1}+{x_2}}}{2}）≤\frac{1}{2}[f（{x_1}）+f（{x_2}）]$，则称f（x）在[a，b]上具有性质P．设f（x）在[1，3]上具有性质P，现给出如下命题：
①f（x）在[1，3]上的图象是连续不断的；
②f（x²）在$[1，\;\sqrt{3}]$上具有性质P；
③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1，3]；
④任意x₁，x₂，x₃，x₄∈[1，3]，有$f（\frac{{{x_1}+{x_2}+{x_3}+{x_4}}}{4}）≤\frac{1}{4}[f（{x_1}）+f（{x_2}）+f（{x_3}）+f（{x_4}）]$．
其中真命题的序号是（　　）

15．双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的焦点坐标为（　　）

（±$\sqrt{7}$，0）

（0，±$\sqrt{7}$）

12．设数列{a_n}的前n项和S由如下程序框图给出，若输入n的值为100，求输出的S．

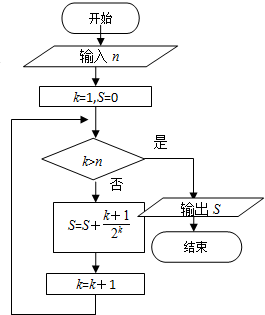
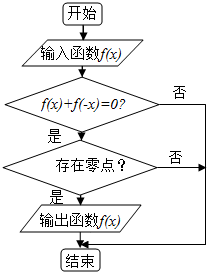某程序框图如图所示，现输入如下四个函数，其中可以输出的函数是f（x）=sinx．
A、f（x）=x²
B、f（x）=$\frac{1}{x}$
C、f（x）=lnx+2x-6
D、f（x）=sinx．