[题目]三个数a.b.c∈(0. ).且cosa=a.sin=c.则a.b.c从小到大的顺序是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】三个数a、b、c∈（0，），且cosa=a，sin（cosb）=b，cos（sinc）=c，则a、b、c从小到大的顺序是．

【答案】b＜a＜c
【解析】解：先证明当x∈（0，）时，sinx＜x 设y=sinx﹣x，则y′=cosx﹣1＜0，∴y=sinx﹣x为（0，）上的减函数，∴y＜sino﹣0=0，即sinx＜x
同理可证明f（x）=sin（cosx）﹣x为（0，）上的减函数，g（x）=cos（sinx）﹣x为（0，）上的减函数
∵sina＜a
∴cos（sina）﹣a=cos（sina）﹣cosa＞0，而cos（sinc）﹣c=0，
∴g（a）＞g（c），a、c∈（0，），
∴a＜c
同理∵x∈（0，）时，sinx＜x，∴sin（cosa）＜cosa
∴sin（cosa）﹣a=sin（cosa）﹣cosa＜0，而sin（cosb）﹣b=0
∴f（a）＜f（b），a、b∈（0，），
∴a＞b
综上所述，b＜a＜c
所以答案是b＜a＜c

练习册系列答案

相关题目

【题目】已知集合A={x|a﹣1＜x＜2a+1}，B={x|0＜x＜1}
（1）若a= ，求A∩B．
（2）若A∩B=，求实数a的取值范围．

【题目】在平面直角坐标系xOy中，满足x2+y2≤1，x≥0，y≥0的点P（x，y）的集合对应的平面图形的面积为；类似的，在空间直角坐标系O﹣xyz中，满足x2+y2+z2≤1，x≥0，y≥0，z≥0的点P（x，y，z）的集合对应的空间几何体的体积为（）
A.
B.
C.
D.

【题目】已知函数是奇函数，f（x）=lg（10x+1）+bx是偶函数．
（1）求a和b的值．
（2）说明函数g（x）的单调性；若对任意的t∈[0，+∞），不等式g（t2﹣2t）+g（2t2﹣k）＞0恒成立，求实数k的取值范围．
（3）设，若存在x∈（﹣∞，1]，使不等式g（x）＞h[lg（10a+9）]成立，求实数a的取值范围．

【题目】某市政府为了确定一个较为合理的居民用电标准，必须先了解全市居民日常用电量的分布情况．现采用抽样调查的方式，获得了n位居民在2012年的月均用电量（单位：度）数据，样本统计结果如下图表：

分组	频数	频率
[0，10）		0.05
[10，20）		0.10
[20，30）	30
[30，40）		0.25
[40，50）		0.15
[50，60]	15
合计	n	1

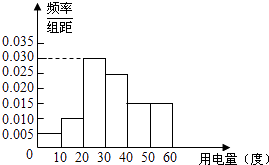
（1）求月均用电量的中位数与平均数估计值；
（2）如果用分层抽样的方法从这n位居民中抽取8位居民，再从这8位居民中选2位居民，那么至少有1位居民月均用电量在30至40度的概率是多少？
（3）用样本估计总体，把频率视为概率，从这个城市随机抽取3位居民（看作有放回的抽样），求月均用电量在30至40度的居民数X的分布列．