题目内容
9.销售甲、乙两种商品所得利润分别是P和Q,它们与投入资金t的关系有经验公式P=$\frac{1}{5}$t,Q=$\frac{12}{5}$$\root{3}{t}$,今将10万元资金投入经营甲、乙两种商品,其中对乙种商品投资x万元,x∈[0,10],(1)试建立总利润y关于x的函数关系式;
(2)试问怎样投资,才能使得总利润最大?并求出该最大值.(其中P,Q,t,x,y的单位均为万元)
分析 (1)根据题意,对乙种商品投资x(万元),对甲种商品投资(10-x)(万元),利用公式P=$\frac{1}{5}$t,Q=$\frac{12}{5}$$\root{3}{t}$,可求经营甲、乙两种商品的总利润y(万元)关于x的函数表达式;
(2)利用导数法,分析函数的单调性,进而可求总利润y的最大值
解答 解:(1)根据题意,对乙种商品投资x(万元),对甲种商品投资(3-x)(万元).
P=$\frac{1}{5}$(10-x),Q=$\frac{12}{5}$$\root{3}{x}$,
可得y=$\frac{1}{5}$(10-x)+$\frac{12}{5}$$\root{3}{x}$=2-$\frac{1}{5}$x+$\frac{12}{5}$$\root{3}{x}$,x∈[0,10],
(2)由(1)得:y′=-$\frac{1}{5}$+$\frac{4}{5}$ ${x}^{-\frac{2}{3}}$,x∈[0,10],
令y′=0,解得:x=8,
∵当x∈[0,8]时,y′>0,原函数为增函数;
当x∈[8,10]时,y′<0,原函数为减函数;
∴当x=8时,y最大值=$\frac{26}{5}$.
答:对甲种商品投资2万元,对乙种商品投资8万元时,总利润的最大值是$\frac{26}{5}$万元. …12
点评 本题考查利用数学知识解决实际问题,考查函数的最值,正确建立函数解析式是关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
14.命题“所有实数的平方根都是正数”的否定为( )
| A. | 所有实数的平方都不是正数 | B. | 有的实数的平方是正数 | ||
| C. | 至少有一个实数的平方不是正数 | D. | 至少有一个实数的平方是正数 |
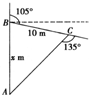 如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10m到达C处发现另一个生命迹象,这是它向右转135°可回到出发点,那么x=$\frac{10\sqrt{6}}{3}$(单位:m).
如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10m到达C处发现另一个生命迹象,这是它向右转135°可回到出发点,那么x=$\frac{10\sqrt{6}}{3}$(单位:m).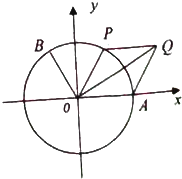 如图,点A是单位圆与x轴正半轴的交点,点B是单位圆上一个定点,点P是一个动点,且∠AOB=120°,∠AOP=θ(0<θ<π),$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.
如图,点A是单位圆与x轴正半轴的交点,点B是单位圆上一个定点,点P是一个动点,且∠AOB=120°,∠AOP=θ(0<θ<π),$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.