题目内容
4.已知:1=1;
1-2=-1;
1-2+3=2;
1-2+3-4=-2;
1-2+3-4+5=3;
…
按此规律请写出第100个等式:1-2+3-4+…+99-100=-50.
分析 由已知中的等式,分析等式右边的值与等差最后一项的关系,并归纳出一般性的规律,可得答案.
解答 解:由已知中:
1=1;
1-2=-1;
1-2+3=2;
1-2+3-4=-2;
1-2+3-4+5=3;
…
归纳可得:
当n为奇数时,不妨令n=2k-1,k∈Z,则1-2+3-4+5-6+…+2k-1=k;
当n为偶数时,不妨令n=2k,k∈Z,则1-2+3-4+5-6+…+2k-1-2k=-k;
故第100个等式为:1-2+3-4+…+99-100=-50,
故答案为:1-2+3-4+…+99-100=-50
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
14.将函数y=$\frac{\sqrt{2}}{2}$(sinx+cosx)的图象上各点的横坐标伸长到原来的2倍,再向左平移$\frac{π}{2}$个单位,所得函数图象的解析式是( )
| A. | y=cos$\frac{x}{2}$ | B. | y=sin($\frac{x}{2}+\frac{3π}{4}$) | C. | y=-sin(2x+$\frac{π}{4}$) | D. | y=sin(2x+$\frac{3π}{4}$) |
12.已知菱形ABCD的边长为a,∠ABC=120°,则$\overrightarrow{BD}$•$\overrightarrow{CD}$=( )
| A. | -$\frac{1}{2}$a2 | B. | -$\frac{3}{2}$a2 | C. | $\frac{1}{2}$a2 | D. | $\frac{3}{2}$a2 |
16.某几何体的三视图如图,则该几何体的体积为( )
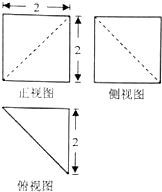

| A. | $\frac{8}{3}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
13.在△ABC中,AB=2,BC=2.5,∠ABC=120°,若使△ABC绕直线BC旋转一周,则所形成的几何体的体积是( )
| A. | $\frac{9π}{2}$ | B. | $\frac{7π}{2}$ | C. | $\frac{5π}{2}$ | D. | $\frac{3π}{2}$ |