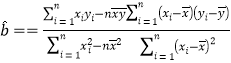题目内容
【题目】某经销商计划销售一款新型的电子产品,经市场调研发现以下规律:当每台电子产品的利润为x(单位:元,x>0)时,销售量q(x)(单位:百台)与x的关系满足:若x不超过25,则q(x)=![]() ;若x大于或等于225,则销售量为零;当25≤x≤225时,q(x)=a-b
;若x大于或等于225,则销售量为零;当25≤x≤225时,q(x)=a-b![]() (a,b为实常数).
(a,b为实常数).
(1) 求函数q(x)的表达式;
(2) 当x为多少时,总利润(单位:元)取得最大值,并求出该最大值.
【答案】(1)见解析;(2)当x等于100元时,总利润取得最大值2000 000元.
【解析】
(1)由分段函数分界点处函数值相等列方程组,可得到![]() ,从而可得函数
,从而可得函数![]() 的表达式;(2)结合(1))根据总利润为每台的利润乘以销售量,利用导数研究函数的单调性,结合单调性可求得分段函数每段的最大值,最后选择一个最大的为分段函数的最大值可得结果.
的表达式;(2)结合(1))根据总利润为每台的利润乘以销售量,利用导数研究函数的单调性,结合单调性可求得分段函数每段的最大值,最后选择一个最大的为分段函数的最大值可得结果.
(1) 当25≤x≤225时,由![]() 得
得![]()
故q(x)=
(2) 设总利润f(x)=x·q(x),
由(1)得f(x)=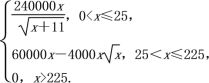
当0<x≤25时,f(x)=![]() =240 000[
=240 000[![]() -
-![]() ],f(x)在(0,25]上单调递增,
],f(x)在(0,25]上单调递增,
所以当x=25时,f(x)有最大值1000 000. 当25<x≤225时,f(x)=60 000x-4000x![]() ,f (x)=60 000-6000
,f (x)=60 000-6000![]() ,
,
令f (x)=0,得x=100.
当25<x<100时,f (x)>0,f(x)单调递增,
当100<x≤225时,f (x)<0,f(x)单调递减,
所以当x=100时,f(x)有最大值2000 000.
当x>225时,f(x)=0.
答:当x等于100元时,总利润取得最大值2000 000元.

【题目】某机构为研究学生玩电脑游戏和对待作业量态度的关系,随机抽取了100名学生进行调查,所得数据如下表所示:
认为作业多 | 认为作业不多 | 总计 | |
喜欢玩电脑游戏 | 25 | 15 | 40 |
不喜欢玩电脑游戏 | 25 | 35 | 60 |
总计 | 50 | 50 | 100 |
(参考公式![]() ,可能用到数据:
,可能用到数据:![]() ,
,![]() ),参照以上公式和数据,得到的正确结论是( )
),参照以上公式和数据,得到的正确结论是( )
A. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度有关
的把握认为喜欢玩电脑游戏与对待作业量的态度有关
B. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度无关
的把握认为喜欢玩电脑游戏与对待作业量的态度无关
C. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度有关
的把握认为喜欢玩电脑游戏与对待作业量的态度有关
D. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度无关
的把握认为喜欢玩电脑游戏与对待作业量的态度无关