题目内容
(本小题满分10分)
判断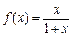 (x∈[0,3])的单调性,并证明你的结论.
(x∈[0,3])的单调性,并证明你的结论.
f(x)在[0,3]上递增,证明略。
解析

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
题目内容
(本小题满分10分)
判断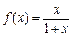 (x∈[0,3])的单调性,并证明你的结论.
(x∈[0,3])的单调性,并证明你的结论.
f(x)在[0,3]上递增,证明略。
解析

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案