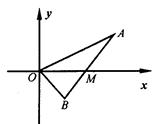
题目内容
 为过抛物线
为过抛物线 焦点
焦点 的一条弦,设
的一条弦,设 ,以下结论正确的是____________________,
,以下结论正确的是____________________,①
 且
且 ②
② 的最小值为
的最小值为 ③以
③以 为直径的圆与
为直径的圆与 轴相切;
轴相切; ①②③
解:因为弦过焦点,因此可以设出直线方程,然后联立方程组,可以得到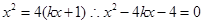 ,因此可以得到①正确
,因此可以得到①正确
同理利用弦长公式可以求解得到 的最小值为
的最小值为 ②正确,对于③,我们利用直角梯形的性质可以得到证明也成立。
②正确,对于③,我们利用直角梯形的性质可以得到证明也成立。
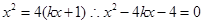 ,因此可以得到①正确
,因此可以得到①正确同理利用弦长公式可以求解得到
 的最小值为
的最小值为 ②正确,对于③,我们利用直角梯形的性质可以得到证明也成立。
②正确,对于③,我们利用直角梯形的性质可以得到证明也成立。
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
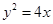 的焦点
的焦点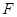 的直线交该抛物线于
的直线交该抛物线于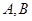 两点,若
两点,若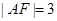 ,则
,则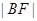 =______
=______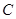 过点
过点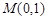 且与直线
且与直线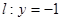 相切,设圆心
相切,设圆心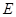 ,
,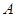 、
、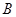 为曲线
为曲线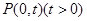 ,且满足
,且满足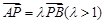 .
.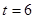 ,直线
,直线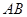 的斜率为
的斜率为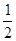 ,过
,过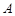 、
、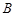 两点的圆
两点的圆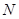 与抛物线在点
与抛物线在点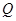 ,若点
,若点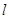 上,求证:
上,求证: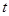 与
与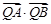 均为定值.
均为定值.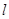 与抛物线
与抛物线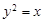 交于
交于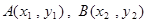 两点,与
两点,与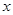 轴相交于点
轴相交于点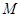 ,且
,且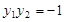 .
.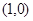 ;
;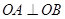 ;
;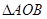 的面积的最小值.
的面积的最小值.
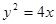 的焦点为F,点P(2,0),O为坐标原点,过P的直线
的焦点为F,点P(2,0),O为坐标原点,过P的直线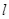 与抛物线C相交于A,B两点,若向量
与抛物线C相交于A,B两点,若向量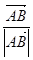 在向量
在向量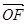 上的投影为n,且
上的投影为n,且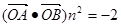 ,求直线
,求直线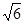 m
m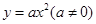 的焦点坐标为
的焦点坐标为 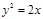 与过焦点的直线l交于A、B两点,则
与过焦点的直线l交于A、B两点,则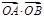 等于( ).
等于( ).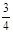 B.
B. 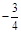 C. 3 D. -2
C. 3 D. -2