题目内容
小区统计部门随机抽查了区内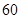 名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过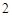 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过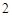 千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为
千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为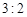 .
.
(1)确定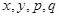 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).
(2)为进一步了解这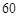 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定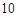 人,若需从这
人,若需从这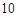 人中随机选取
人中随机选取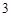 人进行问卷调查,设
人进行问卷调查,设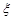 为选取的
为选取的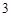 人中“网购红人”的人数,求
人中“网购红人”的人数,求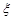 的分布列和数学期望.
的分布列和数学期望.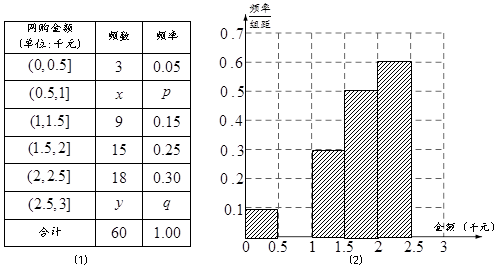
(1) ,
,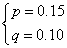 ,补全频率分布直方图如图所示.
,补全频率分布直方图如图所示.
(2)分布列为
 .
.
解析试题分析:(1) “非网购红人”与“网购红人”人数比恰为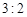 ,又总人数为60,由此可得一个方程组,解这个方程组可得:
,又总人数为60,由此可得一个方程组,解这个方程组可得: ,进而可得:
,进而可得: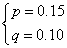 .这样便可补全频率分布直方图;
.这样便可补全频率分布直方图;
(2)选出的人中,“网购红人”有4人,“非网购红人”有6人,从中取3人,故“网购红人”的人数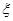 的可能取值为0,1,2,3,这是一个超几何分布,由超几何分布的概率公式可得其分布列,进而求得其期望.
的可能取值为0,1,2,3,这是一个超几何分布,由超几何分布的概率公式可得其分布列,进而求得其期望.
(1) “非网购红人”与“网购红人”人数比恰为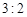 ,所以
,所以 ,
,
又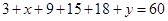 ,解这个方程组得:
,解这个方程组得: .从而可得:
.从而可得: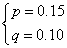 .
.
补全频率分布直方图如图所示:
(2)选出的人中,“网购红人”有4人,“非网购红人”有6人,故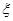 的可能取值为0,1,2,3,
的可能取值为0,1,2,3,
因为 ,
, ,
,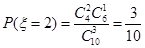 ,
, ,
,
所以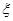 的分布列为:
的分布列为:
 .
.
考点:1、频率分布直方图;2、随机变量的分布列及期望.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个 的列联表;(2)试判断成绩与班级是否有关?
的列联表;(2)试判断成绩与班级是否有关?
参考公式: ;
;
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
为调查民营企业的经营状况,某统计机构用分层抽样的方法从A、B、C三个城市中,抽取若干个民营企业组成样本进行深入研究,有关数据见下表:(单位:个)
| 城市 | 民营企业数量 | 抽取数量 |
| A |  | 4 |
| B | 28 |  |
| C | 84 | 6 |
(1)求
 、
、 的值;
的值;(2)若从城市A与B抽取的民营企业中再随机选2个进行跟踪式调研,求这2个都来自城市A的概率.
想象一下一个人从出生到死亡,在每个生日都测量身高,并作出这些数据的散点图,这些点将不会落在一条直线上,但在一段时间内的增长数据有时可以用线性回归来分析,下表是一位母亲给儿子做的成长记录:
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| | |||||||
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
(2)如果年龄相差5岁,则身高有多大差异(3~16岁之间)?
(3)如果身高相差20 cm,其年龄相差多少(3~16岁之间)?
(4)计算残差,说明该函数模型是否能够较好地反映年龄与身高的关系,说明理由.
 列联表;
列联表;
 和样本方差
和样本方差 (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表); 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 近似为样本方差
近似为样本方差 ;
; 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间 的产品件数.利用(i)的结果,求
的产品件数.利用(i)的结果,求 .
.
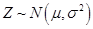 则
则 ,
, 。
。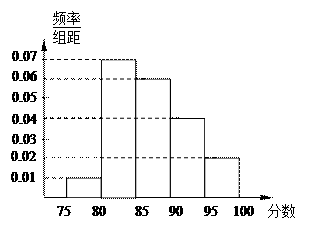
 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6. 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。