题目内容
为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如下表l,表2.
表1:男生“智力评分”频数分布表
| 智力评分 | 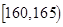 | 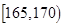 | 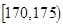 | 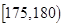 | 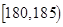 | 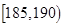 |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生“智力评分”频数分布表
| 智力评分 | 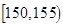 | 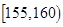 | 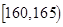 | 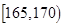 | 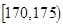 | 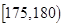 |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)求高一的男生人数并完成下面男生的频率分布直方图;
(2)估计该校学生“智力评分”在[1 65,1 80)之间的概率;
(3)从样本中“智力评分”在[180,190)的男生中任选2人,求至少有1人“智力评分”在[185,190)之间的概率.
(1)高一的男生人数是
男生的频率分布直方图如图所示: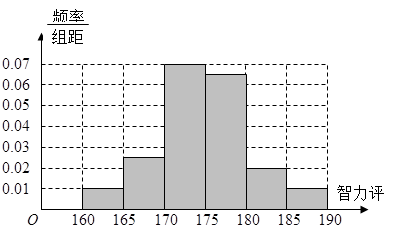
(2)P=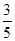 ;
;
(3)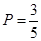 .
.
解析试题分析:(1)样本中男生人数是 ,由抽样比例是10%可得高一的男生人数是
,由抽样比例是10%可得高一的男生人数是 ,
,
根据频率分布表可得,男生的频率分布直方图如图所示.
(2)根据前表得到样本的容量是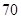 ,计算得到样本中学生“智力评分”在
,计算得到样本中学生“智力评分”在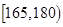 之间的频率为
之间的频率为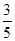 ,
,
由 估计学生“智力评分”在
估计学生“智力评分”在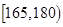 之间的概率是
之间的概率是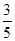 .
.
(3)样本中智力评分”在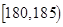 之间的有4人,设其编号是
之间的有4人,设其编号是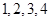 ,样本中“智力评分”在
,样本中“智力评分”在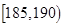 间的男生有
间的男生有 人,设其编号为
人,设其编号为 ,从中任取
,从中任取 人的结果总数是
人的结果总数是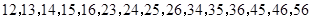 共
共 种,
种,
至少有1人“智力评分”在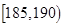 间的有9种.
间的有9种.
(1)样本中男生人数是 ,由抽样比例是10%可得高一的男生人数是
,由抽样比例是10%可得高一的男生人数是 , 1分
, 1分
男生的频率分布直方图如图所示 4分
(2)由表1和表2知,样本中“智力评分”在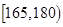 中的人数是
中的人数是 ,样本的容量是
,样本的容量是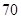 ,所以样本中学生“智力评分”在
,所以样本中学生“智力评分”在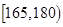 之间的频率
之间的频率 , 6分
, 6分
由 估计学生“智力评分”在
估计学生“智力评分”在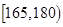 之间的概率是P=
之间的概率是P=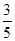 7分
7分
(3)样本中智力评分”在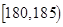 之间的有4人,设其编号是
之间的有4人,设其编号是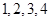 ,样本中“智力评分”在
,样本中“智力评分”在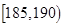 间的男生有
间的男生有 人,设其编号为
人,设其编号为 ,从中任取
,从中任取 人的结果总数是
人的结果总数是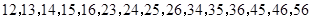 共
共 种, 9分
种, 9分
至少有1人“智力评分”在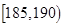 间的有
间的有 种, 11分
种, 11分
因此所求概率是 12分
12分
考点:古典概型,频率分布表,频率分布图.

空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,解代表空气污染越严重:
| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
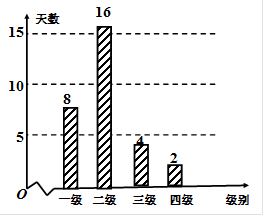
某市2013年3月8日—4月7日(30天)对空气质量指数PM2.5进行检测,获得数据后整理得到如下条形图:
(1)估计该城市一个月内空气质量类别为良的概率;
(2)从空气质量级别为三级和四级的数据中任取2个,求至少有一天空气质量类别为中度污染的概率.
某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
| 组号 | 分组 | 频数 | 频率 |
| 第一组 |  |  |  |
| 第二组 |  |  |  |
| 第三组 |  |  |  |
| 第四组 |  | 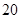 |  |
| 第五组 |  |  |  |
| 合计 |  |  | |
 、
、 、
、 的值;
的值;(2)若从第三、四、五组中用分层抽样方法抽取
 名学生,并在这
名学生,并在这 名学生中随机抽取
名学生中随机抽取 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有 名学生与张老师面谈的概率
名学生与张老师面谈的概率 想象一下一个人从出生到死亡,在每个生日都测量身高,并作出这些数据的散点图,这些点将不会落在一条直线上,但在一段时间内的增长数据有时可以用线性回归来分析,下表是一位母亲给儿子做的成长记录:
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| | |||||||
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
(2)如果年龄相差5岁,则身高有多大差异(3~16岁之间)?
(3)如果身高相差20 cm,其年龄相差多少(3~16岁之间)?
(4)计算残差,说明该函数模型是否能够较好地反映年龄与身高的关系,说明理由.
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) |  |  |  |  |
| 频数(个) | 5 | 10 | 20 | 15 |
 的频率;
的频率;(2)用分层抽样的方法从重量在
 和
和 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在 的有几个?
的有几个?(3)在(2)中抽出的4个苹果中,任取2个,求重量在
 和
和 中各有1个的概率.
中各有1个的概率. 
 和样本方差
和样本方差 (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表); 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 近似为样本方差
近似为样本方差 ;
; 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间 的产品件数.利用(i)的结果,求
的产品件数.利用(i)的结果,求 .
.
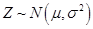 则
则 ,
, 。
。 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6. 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
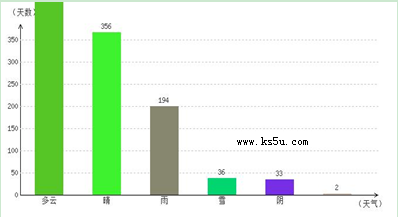
 天,晴
天,晴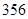 天,雨
天,雨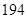 天,雪
天,雪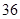 天,阴
天,阴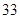 天,其它2天,合计天数为:
天,其它2天,合计天数为: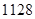 天.
天.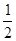 的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为
的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为 元或
元或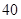 元;在非雨雪天的情况下,他以
元;在非雨雪天的情况下,他以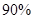 的概率骑自行车上班,每天交通费用
的概率骑自行车上班,每天交通费用 元;另外以
元;另外以 的概率打出租上班,每天交通费用
的概率打出租上班,每天交通费用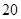 元.(以频率代替概率,保留两位小数. 参考数据:
元.(以频率代替概率,保留两位小数. 参考数据: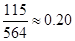 )
)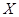 (单位:元),求
(单位:元),求