题目内容
【题目】设函数![]() ,
,
(1)若不等式![]() 的解集为
的解集为![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最小值.
的最小值.
(3)若![]() 求不等式
求不等式![]() 的解集.
的解集.
【答案】(1)2;(2)![]() ;(3)分类讨论,详见解析.
;(3)分类讨论,详见解析.
【解析】
(1)根据不等式与相应的方程之间的关系得出关于![]() 的方程组,求解可得出
的方程组,求解可得出![]() 的值;
的值;
(2)由![]() 得
得![]() ,再代入
,再代入![]() 中运用均值不等式可求得最小值;
中运用均值不等式可求得最小值;
(3)由已知将不等式![]() 化为
化为![]() ,即
,即![]() ,对
,对![]() 分①
分①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 四种情况分别讨论得出不等式的解集.
四种情况分别讨论得出不等式的解集.
(1)由不等式![]() 的解集为
的解集为![]() 可得:方程
可得:方程![]() 的两根为
的两根为![]() ,3且
,3且![]() ,
,
由根与系数的关系可得:![]() ,
,
所以![]()
(2)由已知得![]() ,则
,则
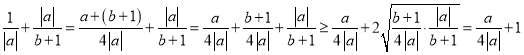 ,
,
当![]() 时,
时,![]() ,所以
,所以![]() (当且仅当
(当且仅当![]() 时等号成立);
时等号成立);
当![]() 时,
时,![]() ,所以
,所以![]() (当且仅当
(当且仅当![]() 时等号成立);
时等号成立);
所以![]() 的最小值为
的最小值为![]() ;
;
(3)由![]() 得
得![]() ,
,
又因为![]() 所以不等式
所以不等式![]() 化为
化为![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,原不等式
,原不等式![]() 或
或![]()
若![]() ,原不等式
,原不等式![]() 此时原不等式的解的情况应由
此时原不等式的解的情况应由![]() 与1的大小关系决定,故
与1的大小关系决定,故
(1)当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ;
;
(2)当![]() 时,
时,![]() ,不等式
,不等式![]()
![]() ;
;
(3)当![]() 时,
时,![]() ,不等式
,不等式![]()
![]() .
.
综上所述,不等式的解集为:
①当![]() 时,
时,![]() 或
或![]() ;
;
②当![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() ;
;
④当![]() 时,
时,![]() .
.
故得解.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目