题目内容
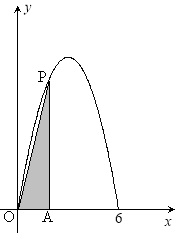
【题目】已知函数![]() ,
,![]()
(1)写出函数![]() 的解析式;
的解析式;
(2)若直线![]() 与曲线
与曲线![]() 有三个不同的交点,求
有三个不同的交点,求![]() 的取值范围;
的取值范围;
(3)若直线 ![]() 与曲线
与曲线![]() 在
在![]() 内有交点,求
内有交点,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]()
![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)先分类讨论求出|f(x)|的解析式,即得函数![]() 的解析式;(2)当
的解析式;(2)当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 只有2个交点,不符题意.当
只有2个交点,不符题意.当![]() 时,由题意得,直线
时,由题意得,直线![]() 与曲线
与曲线![]() 在
在![]() 或
或![]() 内必有一个交点,且在
内必有一个交点,且在![]() 的范围内有两个交点.由
的范围内有两个交点.由![]() 消去
消去![]() 得
得![]() .令
.令![]() ,写出
,写出![]() 应满足条件解得;(3)由方程组
应满足条件解得;(3)由方程组![]() 消去
消去![]() 得
得![]() .由题意知方程在
.由题意知方程在![]() ,
,![]() 内至少有一个实根,设两根为
内至少有一个实根,设两根为![]() ,
,![]() ,不妨设
,不妨设![]() ,
,![]() ,
,![]() .由根与系数关系得
.由根与系数关系得![]() ,
,![]() .代入
.代入![]() 求解即可.
求解即可.
(1)当![]() ,得
,得![]() 或
或![]() ,此时
,此时![]() ;
;
当![]() ,得
,得![]() ,此时
,此时![]()
∴![]()
![]()
(2)当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 只有2个交点,不符题意.
只有2个交点,不符题意.
当![]() 时,由题意得,直线
时,由题意得,直线![]() 与曲线
与曲线![]() 在
在![]() 或
或![]() 内必有一个交点,且在
内必有一个交点,且在![]() 的范围内有两个交点.
的范围内有两个交点.
由![]() ,消去
,消去![]() 得
得![]() .
.
令![]() ,则
,则![]() 应同时满足以下条件:
应同时满足以下条件:
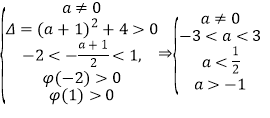 ,
,
解得![]() 或
或![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]()
(3)由方程组![]() ,消去
,消去![]() 得
得![]() .
.
由题意知方程在![]() 内至少有一个实根,设两根为
内至少有一个实根,设两根为![]() ,
,
不妨设![]() ,
,![]() ,由根与系数关系得
,由根与系数关系得![]() ,
,![]()
∴![]()
![]()
![]()
![]()
当且仅当![]() 时取等.
时取等.
所以![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目