题目内容
【题目】已知抛物线C：y=2x2和直线l：y=kx+1，O为坐标原点．
（1）求证：l与C必有两交点；
（2）设l与C交于A（x1 ， y1）、B（x2 ， y2）两点，且直线OA和OB的斜率之和为1，求k的值．
【答案】
（1）证明：抛物线C：y=2x2和直线l：y=kx+1，O为坐标原点，
联立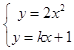 
，得2x2﹣kx﹣1=0，
△=（﹣k）2+8=k2+8＞0，
∴l与C必有两交点．
（2）解：联立 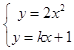，得2x2﹣kx﹣1=0，
△=（﹣k）2+8=k2+8＞0，
设l与C交于A（x1，y1）、B（x2，y2）两点，
则 
，x1x2=﹣ 
，
∵直线OA和OB的斜率之和为1，
∴kOA+kOB= 
= 
= 
= 
= 
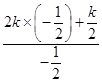=1，
解得k=1
【解析】（1）联立 
，得2x2﹣kx﹣1=0，利用根的判别式能证明l与C必有两交点．（2）联立 ，得2x2﹣kx﹣1=0，设l与C交于A（x1，y1）、B（x2，y2）两点，利用韦达定理、直线的斜率，结合已知条件能求出k的值．
练习册系列答案
相关题目
