题目内容
13.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x,y,则logxy=1的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{36}$ | D. | $\frac{1}{2}$ |
分析 先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x,y,先求出基本事件总数,再求出logxy=1时,x=y,满足条件的基本事件个数,由此能求出logxy=1的概率.
解答 解:先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x,y,
基本事件总数n=6×6=36,
logxy=1时,x=y,满足条件的基本事件个数m=5,
∴logxy=1的概率p=$\frac{m}{n}$=$\frac{5}{36}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
4.一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在B类轿车中抽取一个容量为8的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | z | 400 |
| 标准型 | 300 | 450 | 600 |
(1)求z的值;
(2)用分层抽样的方法在B类轿车中抽取一个容量为8的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
1.如图,在边长为e(e为自然对数的底数)的正方形中,阴影部分的面积为( )
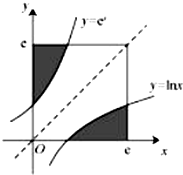

| A. | 2 | B. | $\frac{2}{e}$ | C. | e2 | D. | e |
18.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3-2x2,则f(2)+g(2)=( )
| A. | 16 | B. | -16 | C. | 8 | D. | -8 |
2.已知函数f(x)=ex(x2+ax+1)在点(0,f(0))的切线与直线x-2y+6=0垂直,则a=( )
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |