题目内容
7.已知an=-3n+2,求a1+a4+a7+…+a3n-2.分析 易得a1+a4+a7+…+a3n-2表示首项为-1且公差为-9的等差数列的前n项和,由求和公式可得.
解答 解:∵an=-3n+2,∴数列{an}是首项为-1且公差为-3的等差数列,
∴a1+a4+a7+…+a3n-2表示首项为-1且公差为-9的等差数列的前n项和,
∴由求和公式可得a1+a4+a7+…+a3n-2=-n+$\frac{n(n-1)}{2}$×(-9)=$\frac{-9{n}^{2}+7n}{2}$
点评 本题考查等差数列的求和公式,得出数列的首项和公差是解决问题的关键,属基础题.

练习册系列答案
相关题目
19.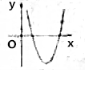 已知函数y=f(x)是偶函数,其部分图象如图所示,则这个函数的零点至少有( )
已知函数y=f(x)是偶函数,其部分图象如图所示,则这个函数的零点至少有( )
 已知函数y=f(x)是偶函数,其部分图象如图所示,则这个函数的零点至少有( )
已知函数y=f(x)是偶函数,其部分图象如图所示,则这个函数的零点至少有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 不确定 |