题目内容
7.f(n)=21+24+27+…+23n+10(n∈N*),则f(n)的项数为n+4.分析 通过观察指数可知有指数构成的数列的通项公式为3n-2,而3n+10为数列的第n+4项,进而可得结论.
解答 解:由题意知,观察指数1,4,7,…,3n+10,
∴该数列的通项公式为an=3n-2,
又∵3n+10为数列的第n+4项,
∴f(n)是首项为2、公比为8的等比数列的前n+4项和,
故答案为:n+4.
点评 本题考查等比数列的简单性质,找出指数数列的公差是解决本题的关键,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
2.已知sinα-sinβ=$\frac{1}{2}$,cosα+cosβ=$\frac{1}{4}$,则cos(α+β)=( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{32}$ | D. | $-\frac{27}{32}$ |
19.已知a=3-2,b=0.3-2,c=log0.32,根据右边程序框图,输出的数是( )
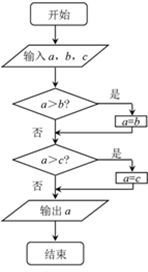

| A. | 3-2 | B. | 0.3-2 | C. | log0.32 | D. | 无法确定 |
16.曲线y=lnx+x-1上的点到直线2x-y+3=0的最短距离是( )
| A. | $\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | $3\sqrt{5}$ | D. | 0 |