题目内容
【题目】为了摸清整个江门大道的交通状况，工作人员随机选取20处路段，在给定的测试时间内记录到机动车的通行数量情况如下（单位：辆）： 147 161 170 180 163 172 178 167 191 182
181 173 174 165 158 154 159 189 168 169
（Ⅰ）完成如下频数分布表，并作频率分布直方图；
通行数量区间 | [145，155） | [155，165） | [165，175） | [175，185） | [185，195） |
频数 |
（Ⅱ）现用分层抽样的方法从通行数量区间为[165，175）、[175，185）及[185，195）的路段中取出7处加以优化，再从这7处中随机选2处安装智能交通信号灯，设所取出的7处中，通行数量区间为[165，175）路段安装智能交通信号灯的数量为随机变量X（单位：盏），试求随机变量X的分布列与数学期望E（X）．
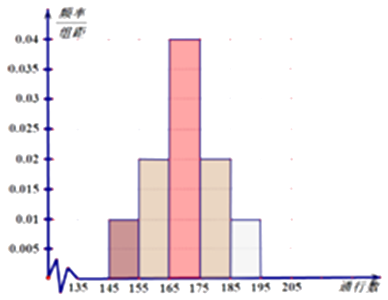
【答案】解：（Ⅰ）
通行数量区间 | [145，155） | [155，165） | [165，175） | [175，185） | [185，195） |
频数 | 2 | 4 | 8 | 4 | 2 |
（Ⅱ）用分层抽样的方法抽取7处，则通行数量区间为[165，175]，
[175，185]，及[185，195）的路段应分别取4处、2处、1处…
依题意，X的可能取值为0，1，2
利用P（X=k）= 
，可得P（X=0）= 
，P（X=1）= 
，P（X=2）= 
．
∴随机变量X的分布列为：
X | 0 | 1 | 2 |
P |
|
|
|
EX=0+1× +2× = 
． 
【解析】（I）利用已知数据即可得出；（II）用分层抽样的方法抽取7处，即可得出．利用P（X=k）= 
，即可得出．
【考点精析】利用频率分布直方图和离散型随机变量及其分布列对题目进行判断即可得到答案，需要熟知频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息；在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．
