题目内容
如图,点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,BC的中点坐标是(11,-4).
(1)求抛物线的方程和焦点F的坐标;
(2)求BC所在直线的方程.

(1)求抛物线的方程和焦点F的坐标;
(2)求BC所在直线的方程.

(1)把A(2,8)代入抛物线方程可得:82=2p×2,
解得p=16,
∴抛物线的方程为y2=32x.
∴焦点F(8,0).
(2)∵B(x1,y1),C(x2,y2)在抛物线y2=32x上,
∴
,
化为(y1+y2)(y1-y2)=32(x1-x2),
∵
=kBC,
=-4,
∴-8kBC=32,
解得kBC=-4.
∴直线BC的方程为y+4=-4(x-11),
化为4x+y-40=0.
解得p=16,
∴抛物线的方程为y2=32x.
∴焦点F(8,0).
(2)∵B(x1,y1),C(x2,y2)在抛物线y2=32x上,
∴
|
化为(y1+y2)(y1-y2)=32(x1-x2),
∵
| y1-y2 |
| x1-x2 |
| y1+y2 |
| 2 |
∴-8kBC=32,
解得kBC=-4.
∴直线BC的方程为y+4=-4(x-11),
化为4x+y-40=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
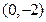 的直线与抛物线
的直线与抛物线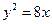 交于
交于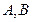 两点,若线段
两点,若线段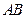 中点的横坐标为
中点的横坐标为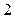 ,求
,求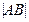 。
。