题目内容

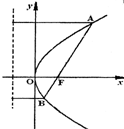
已知抛物线y2=8x上，定点A（3，2），F抛物线的焦点，P为抛物线上的动点，则|PF|+|PA|的最小值为（　　）
A．5B．6C．7D．8
设点A在准线上的射影为D，由抛物线的定义可知|PF|=|PD|
∴要求|PF|+|PA|的最小值，即求|PD|+|PA|的最小值，
只有当D，P，A三点共线时|PD|+|PA|最小，且最小值为3-（-2）=5 （准线方程为x=-2）
故选A
练习册系列答案
相关题目
如图，点A（2，8），B（x1，y1），C（x2，y2）在抛物线y2=2px上，BC的中点坐标是（11，-4）．
（1）求抛物线的方程和焦点F的坐标；
（2）求BC所在直线的方程．
如图，已知AB是过抛物线y2=2px（p＞0）的焦点的弦，F为抛物线的焦点，点A（x1，y1），B（x2，y2）．
求证：
（1）|AB|=x1+x2+p；
（2）y1y2=-p2，x1x2=
p2
4
；
（3）（理科）直线的倾斜角为θ时，求弦长|AB|．
（3）（文科）当p=2，直线AB的倾斜角为
π
4
时，求弦长|AB|．
抛物线x2=8y的准线方程为（　　）
A．y=2B．y=-2C．x=-2D．x=2
若抛物线x=
1
4
y2上的点P（x0，y0）到该抛物线的焦点距离为6，则点P的横坐标为（　　）
A．5B．6C．4D．7
F是抛物线y2=2x的焦点，P是抛物线上任一点，A（3，1）是定点，则|PF|+|PA|的最小值是（　　）
A．2B．
7
2
C．3D．
1
2
已知抛物线y2=2x，
（1）设点A的坐标为(
2
3
，0)，求抛物线上距离点A最近的点P的坐标及相应的距离|PA|；
（2）在抛物线上求一点P，使P到直线x-y+3=0的距离最短，并求出距离的最小值．
抛物线y2=2x上一点M到焦点的距离为1，则点M的横坐标是______．
抛物线y=ax2的准线方程是y=1，则a的值为（　　）
A．
1
4
B．-
1
4
C．4D．-4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网