题目内容
【题目】已知函数![]() .
.
(1)求![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,证明:
时,证明:![]() ;
;
(3)判断曲线![]() 与
与![]() 是否存在公切线,若存在,说明有几条,若不存在,说明理由.
是否存在公切线,若存在,说明有几条,若不存在,说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)存在;存在2条公切线
;(2)证明见解析;(3)存在;存在2条公切线
【解析】
(1)计算![]() ,根据曲线在该点处导数的几何意义可得切线的斜率,然后计算
,根据曲线在该点处导数的几何意义可得切线的斜率,然后计算![]() ,利用点斜式,可得结果.
,利用点斜式,可得结果.
(2)分别构造![]() ,通过导数研究
,通过导数研究![]() 的性质,可得
的性质,可得 ![]() ,
,![]() ,简单判断,可得结果.
,简单判断,可得结果.
(3)分别假设![]() 与
与![]() 的切线,根据公切线,可得
的切线,根据公切线,可得![]() ,利用导数研究函数
,利用导数研究函数![]() 零点个数,根据
零点个数,根据![]() 性质可得结果.
性质可得结果.
解:(1)![]() 的定义域
的定义域![]()
![]()
又![]()
所以![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]() .
.
(2)设![]() ,
,
![]() ,
,
![]()
|
|
|
|
|
|
|
|
| ↑ | 极大值 | ↓ |
![]()
![]()
设![]() 则
则![]() 在
在![]() 上恒成立
上恒成立
![]()
![]()
综上![]()
(3)曲线![]() 与
与![]() 存在公切线,且有2条,理由如下:
存在公切线,且有2条,理由如下:
由(2)知曲线![]() 与
与![]() 无公共点,
无公共点,
设![]() 分别切曲线
分别切曲线![]() 与
与![]() 于
于![]() ,则
,则
![]() ,
,
若![]() ,即曲线
,即曲线![]() 与
与![]() 有公切线,则
有公切线,则
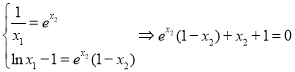
令![]() ,
,
则曲线![]() 与
与![]() 有公切线,当且仅当
有公切线,当且仅当![]() 有零点,
有零点,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减
单调递减
![]() ,
,
所以存在![]() ,使得
,使得![]()
且当![]() 时,
时,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() 单调递减
单调递减
![]() ,
,
又![]()
所以![]() 在
在![]() 内各存在有一个零点
内各存在有一个零点
故曲线![]() 与
与![]() 存在2条公切线.
存在2条公切线.

【题目】某传染病疫情爆发期间,当地政府积极整合医疗资源,建立“舱医院”对所有密切接触者进行14天的隔离观察治疗.治疗期满后若检测指标仍未达到合格标准,则转入指定专科医院做进一步的治疗.“舱医院”对所有人员在“入口”及“出口”时都进行了医学指标检测,若“入口”检测指标在35以下者则不需进入“舱医院”而是直接进入指定专科医院进行治疗.以下是20名进入“舱医院”的密切接触者的“入口”及“出口”医学检测指标:
入口 | 50 | 35 | 35 | 40 | 55 | 90 | 80 | 60 | 60 | 60 | 65 | 35 | 60 | 90 | 35 | 40 | 55 | 50 | 65 | 50 |
出口 | 70 | 50 | 60 | 50 | 75 | 70 | 85 | 70 | 80 | 70 | 55 | 50 | 75 | 90 | 60 | 60 | 65 | 70 | 75 | 70 |
(Ⅰ)建立![]() 关于
关于![]() 的回归方程;(回归方程的系数精确到0.1)
的回归方程;(回归方程的系数精确到0.1)
(Ⅱ)如果60是“舱医院”的“出口”最低合格指标,那么,“入口”指标低于多少时,将来这些密切接触者将不能进入“舱医院”而是直接进入指定专科医院接受治疗.(检测指标为整数)
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: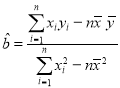 ,
,![]() .
.
【题目】某省级示范高中高三年级对各科考试的评价指标中,有“难度系数“和“区分度“两个指标中,难度系数![]() ,区分度
,区分度![]() .
.
(1)某次数学考试(满分为150分),随机从实验班和普通班各抽取三人,实验班三人的成绩分别为147,142,137;普通班三人的成绩分别为97,102,113.通过样本估计本次考试的区分度(精确0.01).
(2)如表表格是该校高三年级6次数学考试的统计数据:
难度系数x | 0.64 | 0.71 | 0.74 | 0.76 | 0.77 | 0.82 |
区分度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
①计算相关系数r,|r|<0.75时,认为相关性弱;|r|≥0.75时,认为相关性强.通过计算说明,能否利用线性回归模型描述y与x的关系(精确到0.01).
②ti=|xi﹣0.74|(i=1,2,…,6),求出y关于t的线性回归方程,并预测x=0.75时y的值(精确到0.01).
附注:参考数据: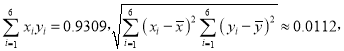
![]()
![]()
参考公式:相关系数 r,回归直线
r,回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为