题目内容
7.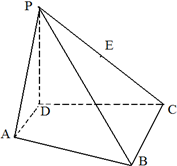 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.(1)若AD=$\frac{1}{2}$BC,E为PC的中点,求证:DE∥平面PAB;
(2)求直线PB与平面PAD所成角的大小.
分析 (1)取中的,利用中位线得出AD∥EM,AD=EM,再利用直线平面的平行问题求解.
(2)建立空间坐标系,求解平面的法向量,利用向量求解sinθ=cos<$\overrightarrow{n}$,$\overrightarrow{PB}$>即可.
解答 解:(1)取PB中点M,连接DE,EM,AM,
∵AD=$\frac{1}{2}$BC,E为PC的中点,
∴EM∥BC,EM=$\frac{1}{2}BC$,
∴AD∥EM,AD=EM,
即四边形ADEM为平行四边形,
∴DE∥AM,
∵ED?平面PAB,AM?平面PAB;
∴DE∥平面PAB;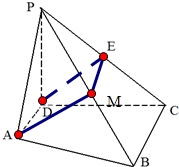
(2)以DA,DC,DP为x,y,z轴,直线PB与平面PAD所成角的大小θ.
PD:DC:BC=1:1:$\sqrt{2}$.
设DC=1,则DP=1,DA=$\frac{\sqrt{2}}{2}$,BC=$\sqrt{2}$,
∴P(0,0,1),A($\frac{\sqrt{2}}{2}$,0,0),B($\sqrt{2}$,1,0),C(0,1,0),D(0,0,0),
∴$\overrightarrow{PB}$=($\sqrt{2}$,1,-1),$\overrightarrow{DA}$=($\frac{\sqrt{2}}{2}$,0,0),$\overrightarrow{DP}$=(0,0,1),
设$\overrightarrow{n}$=(x,y,z),∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DP}=0}\\{\overrightarrow{n}•\overrightarrow{DA}=0}\end{array}\right.$
即x=0,z=0,y=1
∴$\overrightarrow{n}$=(0,1,0),
∵$\overrightarrow{n}$$•\overrightarrow{PB}$=1,|$\overrightarrow{n}$=1,|$\overrightarrow{PB}$|=2,
∴cos<$\overrightarrow{n}$,$\overrightarrow{PB}$>=$\frac{\overrightarrow{PB}•\overrightarrow{n}}{|\overrightarrow{n}|•\overrightarrow{PB}}$=$\frac{1}{2}$,
∴sinθ=$\frac{1}{2}$,
即θ=$\frac{π}{6}$
点评 本题综合考查了空间直线平面的平行问题,运用空间向量求解平面的法向量,夹角问题,注意坐标要计算准确,保证向量的运算不出错.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案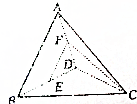 如图,正三棱锥A-BCD中,E、F分别为BD、AD的中点,且EF⊥CF,底面边长为2,则点B到平面ACD的距离为( )
如图,正三棱锥A-BCD中,E、F分别为BD、AD的中点,且EF⊥CF,底面边长为2,则点B到平面ACD的距离为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
 已知点A,B,C都在以原点O为圆心点的圆上,其中$\overrightarrow{OA}$=(-3,4),点B位于第一象限,点C为圆O与x轴正半轴的交点,若△BOC为正三角形.
已知点A,B,C都在以原点O为圆心点的圆上,其中$\overrightarrow{OA}$=(-3,4),点B位于第一象限,点C为圆O与x轴正半轴的交点,若△BOC为正三角形.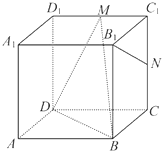 如图,正方体ABCD-A1B1C1D1的棱长为2,M,N分别是C1D1,CC1的中点,则直线B1N与平面BDM所成角的正弦值为$\frac{{\sqrt{5}}}{3}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,M,N分别是C1D1,CC1的中点,则直线B1N与平面BDM所成角的正弦值为$\frac{{\sqrt{5}}}{3}$. 如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,0是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,0是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.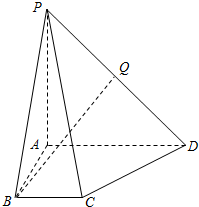 在四棱锥P-ABCD中,PA⊥平面ABCD,底面四边形ABCD为直角梯形,AD∥BC,AD⊥AB,PA=AD=2,AB=BC=1,Q为PD中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面四边形ABCD为直角梯形,AD∥BC,AD⊥AB,PA=AD=2,AB=BC=1,Q为PD中点. 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.