题目内容
15. 如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,0是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,0是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.(Ⅰ)求证:直线SA∥平面BDE;
(Ⅱ)求二面角D-SB-C的余弦值.
分析 (Ⅰ)连接OE,利用正方形的性质与三角形中位线定理可得:OE∥SA.再利用线面平行的判定定理可得:直线SA∥平面BDE;
(II)建立如图所示的空间直角坐标系,由∠SAO=45°.可得D$(0,-2\sqrt{2},0)$,B$(0,2\sqrt{2},0)$,S$(0,0,2\sqrt{2})$,C$(-2\sqrt{2},0,0)$.设平面SBC的法向量$\overrightarrow{n}$=(x,y,1),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{SB}=0}\\{\overrightarrow{n}•\overrightarrow{BC}=0}\end{array}\right.$,可得$\overrightarrow{n}$.取平面SBD的法向量为$\overrightarrow{OC}$,利用$cos<\overrightarrow{OC},\overrightarrow{n}>$=$\frac{\overrightarrow{OC}•\overrightarrow{n}}{|\overrightarrow{OC}||\overrightarrow{n}|}$,即可得出.
解答 (Ⅰ)证明:连接OE,
∵四边形ABCD是正方形,∴OC=OA,
又E是侧棱SC的中点,∴OE∥SA.
又SA?平面BDE,OE?平面BDE,
∴直线SA∥平面BDE;
(II)解:建立如图所示的空间直角坐标系,
∵∠SAO=45°.∴D$(0,-2\sqrt{2},0)$,B$(0,2\sqrt{2},0)$,S$(0,0,2\sqrt{2})$,C$(-2\sqrt{2},0,0)$.
$\overrightarrow{OC}$=$(-2\sqrt{2},0,0)$,$\overrightarrow{BC}$=$(-2\sqrt{2},-2\sqrt{2},0)$,$\overrightarrow{SB}$=$(0,2\sqrt{2},-2\sqrt{2})$.
设平面SBC的法向量$\overrightarrow{n}$=(x,y,1),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{SB}=0}\\{\overrightarrow{n}•\overrightarrow{BC}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{2\sqrt{2}y-2\sqrt{2}=0}\\{-2\sqrt{2}x-2\sqrt{2}y=0}\end{array}\right.$,取$\overrightarrow{n}$=(-1,1,1).
取平面SBD的法向量为$\overrightarrow{OC}$=$(-2\sqrt{2},0,0)$.
$cos<\overrightarrow{OC},\overrightarrow{n}>$=$\frac{\overrightarrow{OC}•\overrightarrow{n}}{|\overrightarrow{OC}||\overrightarrow{n}|}$=$\frac{2\sqrt{2}}{\sqrt{3}×2\sqrt{2}}$=$\frac{\sqrt{3}}{3}$.
∴二面角D-SB-C的余弦值为$\frac{\sqrt{3}}{3}$.
点评 本题考查了三角形中位线定理、正方形的性质定理、线面平行的判定定理、向量与数量积的关系、法向量与空间角的求法,考查了推理能力与计算能力,属于中档题.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案| A. | 199 | B. | 2100-1 | C. | 2101-1 | D. | 2100 |
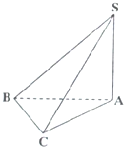 如图,在三棱锥S-ABC中,SA⊥底面ABC,AC⊥BC,若AC=BC=1,SA=AB,则SB与平面SAC所成角的大小为30°.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AC⊥BC,若AC=BC=1,SA=AB,则SB与平面SAC所成角的大小为30°. 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1. 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$. 在如图所示的空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为A1D1和A1B1的中点.
在如图所示的空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为A1D1和A1B1的中点.