题目内容
【题目】已知实数x，y满足 
，则目标函数2x+y的最大值为 ， 目标函数4x2+y2的最小值为 ．
【答案】10；8
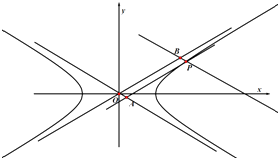
【解析】解：作出不等式组对应的平面区域如图：（阴影部分）．
设z=2x+y得y=﹣2x+z，平移直线y=﹣2x+z，
由图象可知当直线y=﹣2x+z经过点A时，直线y=﹣2x+z的截距最大，
此时z最大．
由 
，解得 
，即A（ 
，5），
代入目标函数z=2x+y得z=2× +5=5+5=10．
即目标函数z=2x+y的最大值为10．
设4x2+y2=m，则m＞0，
即 
+ 
=1，表示焦点在y轴的椭圆，
要使m最小，则只需要椭圆和直线BC：2x+y﹣4=0，相切即可，
由2x+y﹣4=0得y=﹣2x+4代入4x2+y2=m，得4x2+（﹣2x+4）2=m，
即8x2﹣16x+16﹣m=0，
则判别式△=162﹣4×8（16﹣m）=0，
得8=16﹣m，
则m=8，即目标函数4x2+y2的最小值为8，
所以答案是：10，8．
练习册系列答案
阅读快车系列答案
相关题目
