Question

【题目】已知正三角形ABC的边长为2，D、E、F分别是BC、CA、AB的中点．
（1）在三角形内部随机取一点P，求满足|PB|≥1且|PC|≥1的概率；
（2）在A、B、C、D、E、F这6点中任选3点，记这3点围成图形的面积为ξ，求随机变量ξ的分布列与数学期望Eξ．

Answer 1

【答案】
（1）解：如图1所示，

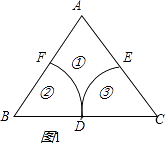
分别以正△ABC的顶点B、C为圆心，以1为半径画圆弧，交边AB、BC、AC于点F、D、E；

则点P在区域①时满足条件|PB|≥1且|PC|≥1，

其概率为P=1﹣ 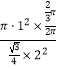=1﹣ =1﹣

（2）解：在A、B、C、D、E、F这6点中任选3点，共有20种不同的取法；

记这3点围成图形的面积为ξ，则ξ=0， S△， S△，S△；其中S△= ；

P（ξ=0）= ，P（ξ= S△）= = ，P（ξ= S△）= = ，P（ξ=S△）= ；

所以随机变量ξ的分布列为：

ξ	0
P

数学期望Eξ=0× + × + × + × =

【解析】（1）根据几何概型的计算公式，求出满足条件|PB|≥1且|PC|≥1的概率值即可；（2）根据题意，求出3点围成图形的面积ξ的可能取值以及对应的概率值，列出ξ的分布列，计算数学期望Eξ的值．
【考点精析】根据题目的已知条件，利用几何概型和离散型随机变量及其分布列的相关知识可以得到问题的答案，需要掌握几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等；在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．