题目内容
1.已知函数f(x)=x2-2|x-a|.(1)若a=1,求不等式f(x)>2x的解集.
(2)若a>0,且方程f(x)=x恰有三个不同的实根,求a的取值范围.
(3)当a>0时,若对任意的x∈[0,+∞),不等式f(x-1)≥2f(x)恒成立,求实数a的取值范围.
分析 (1)若a=1,根据绝对值不等式的解法即可求不等式f(x)>2x的解集
(2)若a>0,方程f(x)=x恰有三个不同的实根,转化为f(x)与g(x)=x有3个不同的交点,利用数形结合进行求解即可求a的值
(3)先整理f(x-1)≤2f(x)的表达式,有绝对值的放到左边,然后分①0≤x≤a②a<x≤1+a③x>1+a讨论,首先去掉绝对值,然后整理成关于x的一元二次不等式恒成立的问题,利用函数的单调性求出最值,从而求出a的范围,最后求它们的交集.
解答 解:(1)若a=1,不等式f(x)>2x等价为x2-2|x-1|>2x.
若x≥1,则不等式等价为x2-2x+2>2x.即x2-4x+2>0,
解得x≥2+$\sqrt{2}$或x≤2-$\sqrt{2}$(舍),
若x<1,则不等式等价为x2+2x-2>2x.即x2-2>0,
解得x>$\sqrt{2}$(舍)或x<-$\sqrt{2}$,
综上x≥2+$\sqrt{2}$或x<-$\sqrt{2}$,
即不等式的解集为{x|x≥2+$\sqrt{2}$或x<-$\sqrt{2}$}.
(2)若a>0,且方程f(x)=x恰有三个不同的实根,
即x2-2|x-a|=x,$\frac{1}{2}$(x2-x)=|x-a|.
设y=$\frac{1}{2}$(x2-x),y=|x-a|.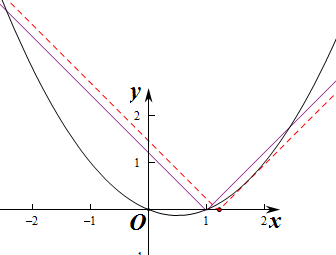
作出函数y=$\frac{1}{2}$(x2-x)和y=|x-a|的图象如图:
当y=|x-a|经过点(1,0)时,即|1-a|=0,
a=1时,满足条件,
当x≥a时,y=|x-a|=x-a,
当直线y=x-a与y=$\frac{1}{2}$(x2-x)相切时,
即y=$\frac{1}{2}$(x2-x)=x-a,
即x2-x=2x-2a,
即x2-3x+2a=0,由判别式△=9-8a=0,
即a=$\frac{9}{8}$时,两个曲线有2个交点,
故方程f(x)=x恰有三个不同的实根,
则1≤a<$\frac{9}{8}$,
即实数a的取值范围是1≤a<$\frac{9}{8}$.
(3)不等式f(x-1)≥2f(x)化为-(x-1)2+2|x-1-a|≥-2x2+4|x-a|,
即:4|x-a|-2|x-(1+a)|≤x2+2x-1(*)
对任意的x∈[0,+∞)恒成立.
因为a>0.所以分如下情况讨论:
①0≤x≤a时,不等式(*)化为-4(x-a)+2[x-(1+a)]≤x2+2x-1,
即x2+4x+1-2a≥0对任意的x∈[0,a]恒成立,
因为函数g(x)=x2+4x+1-2a在区间[0,a]上单调递增,
则g(0)最小,所以只需g(0)≥0即可,得a≤$\frac{1}{2}$,
又a>0所以0<a≤$\frac{1}{2}$,
②a<x≤1+a时,不等式(*)化为4(x-a)+2[x-(1+a)]≤x2+2x-1,
即x2-4x+1+6a≥0对任意的x∈(a,1+a]恒成立,
由①,0<a≤$\frac{1}{2}$,知:函数h(x)=x2-4x+1+6a在区间(a,1+a]上单调递减,
则只需h(1+a)≥0即可,即a2+4a-2≥0,得a≤-2-$\sqrt{6}$或a≥-2+$\sqrt{6}$.
因为-2+$\sqrt{6}$<$\frac{1}{2}$,所以由①得-2+$\sqrt{6}$≤a≤$\frac{1}{2}$,
③x>1+a时,不等式(*)化为4(x-a)-2[x-(1+a)]≥x2+2x-1,
即x2+2a-3≥0对任意的x∈(a+1,+∞)恒成立,
因为函数φ(x)=x2+2a-3在区间(a+1,+∞)上单调递增,
则只需φ(a+1)≥0即可,
即a2+4a-2≥0,得或a≤-2-$\sqrt{6}$或a≥-2+$\sqrt{6}$.
由②得-2+$\sqrt{6}$≤a≤$\frac{1}{2}$,
综上所述得,a的取值范围是[-2+$\sqrt{6}$,$\frac{1}{2}$].
点评 本题主要考查函数恒成立问题,涉及绝对值不等式求解,函数与方程的应用,分段函数以及一元二次函数的图象和性质,综合性较强,难度较大.

 名题金卷系列答案
名题金卷系列答案| A. | 0.5 | B. | 0.4 | C. | 0.3 | D. | 0.2 |
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | -$\frac{1}{4}$ |
| A. | [e,4] | B. | [1,4] | C. | (4,+∞) | D. | (-∞,1] |