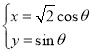题目内容
【题目】如图抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上一点(
为抛物线上一点(![]() 在
在![]() 轴上方),
轴上方),![]() ,
,![]() 点到
点到![]() 轴的距离为4.
轴的距离为4.
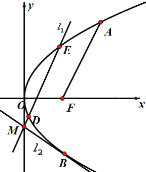
(1)求抛物线方程及点![]() 的坐标;
的坐标;
(2)是否存在![]() 轴上的一个点
轴上的一个点![]() ,过点
,过点![]() 有两条直线
有两条直线![]() ,满足
,满足![]() ,
,![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.![]() 与抛物线相切于点
与抛物线相切于点![]() (
(![]() 不为坐标原点),有
不为坐标原点),有![]() 成立,若存在,求出点
成立,若存在,求出点![]() 的坐标.若不存在,请说明理由.
的坐标.若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ; (2)存在点
; (2)存在点![]() .
.
【解析】
(1)由抛物线的定义,可得![]() ,且
,且![]() ,求得
,求得![]() ,即可得到抛物线的方程,进而得到A点的坐标;
,即可得到抛物线的方程,进而得到A点的坐标;
(2)设![]() 的方程为
的方程为![]() ,联立方程组,由
,联立方程组,由![]() ,解得
,解得![]() ,
,
得到![]() ,再由
,再由![]() 的方程为
的方程为![]() ,联立方程组,求得
,联立方程组,求得![]() ,
,![]() ,结合
,结合![]() ,即可得到结论.
,即可得到结论.
(1)由抛物线![]() 的焦点为
的焦点为![]() ,满足
,满足![]() ,
,![]() 点到
点到![]() 轴的距离为4,由抛物线的定义,可得
轴的距离为4,由抛物线的定义,可得![]() ,且
,且![]() ,解得
,解得![]() ,
,
所以抛物线的方程为![]() ,
,
令![]() ,解得
,解得![]() ,
,
又由![]() 在
在![]() 轴上方,所以
轴上方,所以![]() ,即
,即![]() .
.
(2)假设存在点M,可知直线![]() 的斜率存在,
的斜率存在,
设![]() 的方程为
的方程为![]() ,
,
联立方程组![]() ,整理得
,整理得![]() ,
,
由![]() ,解得
,解得![]() ,
,
此时切点![]() ,可得
,可得![]() ,
,
因为![]() ,所以
,所以![]() 的方程为
的方程为![]() ,
,
联立![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,![]()
![]()
由![]() 可得,
可得,![]() ,解得
,解得![]() ,
,
所以存在点![]() ,符合题意.
,符合题意.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|