题目内容
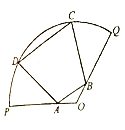
【题目】如图，抛物线
的焦点为
，抛物线
上
两点，在抛物线的准线上的射影分别为
.
（1）如图，若点在线段
上，过
作
的平行线
与抛物线准线交于
，证明：是
的中点；
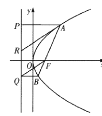
（2）如图，若
的面积是
的面积的两倍，求中点的轨迹方程.
【答案】(1)见解析;(2)
.
【解析】
(1) 设直线
,与抛物线方程联立可得
，∴
.
于是
，直线
，设直线
与
交于点
，令
.
易得
（2）设
与
轴的焦点分别为
，则
，∵
的面积是
的面积的两倍，∴
，所以点
. 可设直线
，与抛物线方程联立可得
∴
，从而可得
,即所求轨迹方程.
（1）由题，
，准线.
设直线，
，
.
联立
，∴.
于是，直线，
设直线与交于点，令.
得：
.
故直线经过的中点.
（2）设与轴的焦点分别为，
则
，
∵的面积是的面积的两倍，
∴，所以点.
可设直线，，
中点
，
，
∴.
于是
，
,
即中点的轨迹方程为.
练习册系列答案
智慧小复习系列答案
相关题目
