题目内容
斜率为2的直线经过抛物线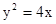 的焦点,与抛物线交与A、B两点,则
的焦点,与抛物线交与A、B两点,则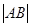 = .
= .
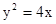 的焦点,与抛物线交与A、B两点,则
的焦点,与抛物线交与A、B两点,则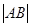 = .
= .5
试题分析:根据已知抛物线的方程可知其焦点坐标为(1,0),则直线方程为y=2(x-1),代入抛物线中,
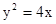 ,得到[2(x-1)]2=4x,x2-3x+1=0,∴x1+x2=3
,得到[2(x-1)]2=4x,x2-3x+1=0,∴x1+x2=3根据抛物线的定义可知|AB| =x1+x2+p=3+2=5
故答案为5.
点评:解决该试题的关键是运用设而不求的思想,设直线方程,并与抛物线联立方程组,结合韦达定理得到弦长的求解,|AB|=x1+
 +x2+
+x2+ 表示的为过焦点的弦长公式要熟练掌握。.
表示的为过焦点的弦长公式要熟练掌握。.
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
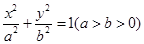 右焦点为
右焦点为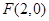 ,M为椭圆的上顶点,O为坐标原点,且
,M为椭圆的上顶点,O为坐标原点,且 是等腰直角三角形,(1)求椭圆的方程(2)过M分别作直线MA,MB,交椭圆于A,B两点,设两直线的斜率分别为
是等腰直角三角形,(1)求椭圆的方程(2)过M分别作直线MA,MB,交椭圆于A,B两点,设两直线的斜率分别为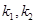 ,且
,且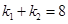 ,证明:直线AB过定点,并求定点的坐标。
,证明:直线AB过定点,并求定点的坐标。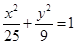 上一点
上一点 到一个焦点的距离为5,则
到一个焦点的距离为5,则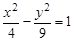 有相同的渐近线,且一条准线为
有相同的渐近线,且一条准线为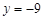 ,求双曲线C的方程;
,求双曲线C的方程; (Ⅱ)已知圆截
(Ⅱ)已知圆截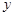 轴所得弦长为6,圆心在直线
轴所得弦长为6,圆心在直线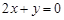 上,并与
上,并与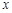 轴相切,求该圆的方程.
轴相切,求该圆的方程. 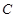 :
: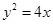 的焦点为
的焦点为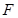 ,直线
,直线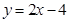 与
与 、
、 两点.则
两点.则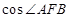 ="________."
="________."  在坐标轴上,离心率为
在坐标轴上,离心率为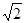 ,且过点(4,-
,且过点(4,-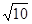 )(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证:
)(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证: .(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分)
.(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分) 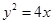 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 两点,点
两点,点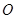 是原点,若
是原点,若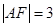 ,则
,则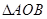 的面积为
的面积为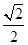



 、
、 ,以
,以 为边作正三角形,若双曲线恰好平分另外两边,则双曲线的离心率为( )
为边作正三角形,若双曲线恰好平分另外两边,则双曲线的离心率为( )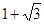
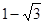

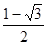
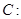
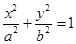
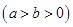 的左右焦点分别是
的左右焦点分别是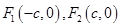 ,直线
,直线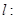
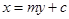 与椭圆
与椭圆 交于两点
交于两点 ,
, .当
.当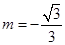 时,M恰为椭圆
时,M恰为椭圆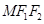 的周长为6.
的周长为6.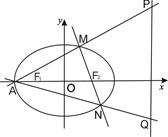
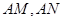 与直线
与直线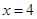 分别相交于点
分别相交于点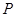 ,
,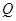 ,问当
,问当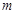
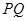 为直径的圆被
为直径的圆被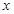 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值,