题目内容
(12分)已知椭圆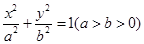 右焦点为
右焦点为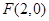 ,M为椭圆的上顶点,O为坐标原点,且
,M为椭圆的上顶点,O为坐标原点,且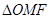 是等腰直角三角形,(1)求椭圆的方程(2)过M分别作直线MA,MB,交椭圆于A,B两点,设两直线的斜率分别为
是等腰直角三角形,(1)求椭圆的方程(2)过M分别作直线MA,MB,交椭圆于A,B两点,设两直线的斜率分别为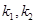 ,且
,且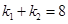 ,证明:直线AB过定点,并求定点的坐标。
,证明:直线AB过定点,并求定点的坐标。
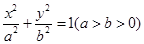 右焦点为
右焦点为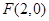 ,M为椭圆的上顶点,O为坐标原点,且
,M为椭圆的上顶点,O为坐标原点,且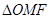 是等腰直角三角形,(1)求椭圆的方程(2)过M分别作直线MA,MB,交椭圆于A,B两点,设两直线的斜率分别为
是等腰直角三角形,(1)求椭圆的方程(2)过M分别作直线MA,MB,交椭圆于A,B两点,设两直线的斜率分别为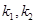 ,且
,且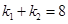 ,证明:直线AB过定点,并求定点的坐标。
,证明:直线AB过定点,并求定点的坐标。(1) 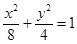 (2)
(2)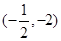
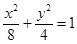 (2)
(2)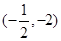
试题分析:(1)由已知可知
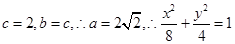
(2)若K存在,设直线AB的方程为
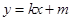 与椭圆方程联立得
与椭圆方程联立得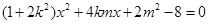
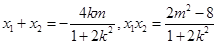 ,因为
,因为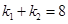
所以
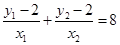 即各解得
即各解得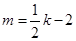 所以AB的方程为
所以AB的方程为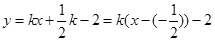 故直线AB过定点,定点坐标为
故直线AB过定点,定点坐标为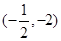 .
.若K不存在A(
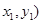 ,B
,B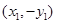 代入
代入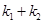 =8解得
=8解得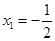 所以直线AB过定点
所以直线AB过定点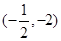 ,综上,直线AB必过定点
,综上,直线AB必过定点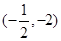
点评:求直线过定点只需将直线整理为含有一个参数的一般方程。

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
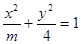 的离心率为
的离心率为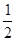 ,则
,则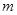 为 .
为 .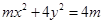 的离心率e为方程
的离心率e为方程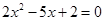 的两根,则满足条件的圆锥曲线的条数为 ( )
的两根,则满足条件的圆锥曲线的条数为 ( )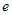 是椭圆
是椭圆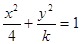 的离心率,且
的离心率,且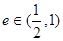 ,则实数
,则实数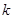 的取值范围是( )
的取值范围是( ) )
) 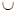 (
( 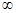 )
)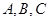 均在椭圆
均在椭圆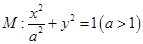 上,直线
上,直线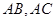 分别过椭圆的左、右焦点
分别过椭圆的左、右焦点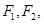 当
当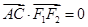 时,有
时,有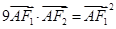
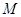 的方程
的方程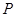 是椭圆
是椭圆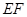 为圆
为圆 的任一条直径,求
的任一条直径,求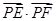 的最大值
的最大值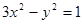 交于A,B两点.
交于A,B两点. 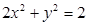 的一个焦点的直线交椭圆于
的一个焦点的直线交椭圆于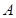 、
、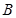 两点,求
两点,求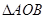 面积的最大值.(
面积的最大值.(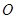 为坐标原点)
为坐标原点)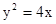 的焦点,与抛物线交与A、B两点,则
的焦点,与抛物线交与A、B两点,则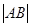 = .
= .