题目内容
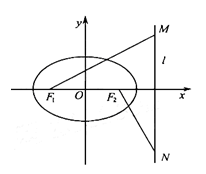
已知椭圆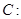
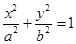
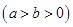 的左右焦点分别是
的左右焦点分别是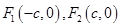 ,直线
,直线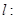
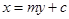 与椭圆
与椭圆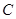 交于两点
交于两点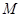 ,
,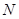 .当
.当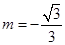 时,M恰为椭圆
时,M恰为椭圆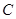 的上顶点,此时△
的上顶点,此时△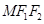 的周长为6.
的周长为6.
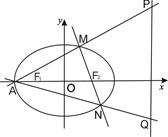
(Ⅰ)求椭圆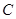 的方程;
的方程;
(Ⅱ)设椭圆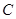 的左顶点为A,直线
的左顶点为A,直线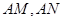 与直线
与直线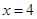 分别相交于点
分别相交于点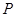 ,
,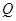 ,问当
,问当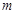
变化时,以线段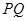 为直径的圆被
为直径的圆被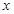 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值,
若不是,说明理由.
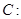
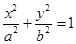
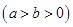 的左右焦点分别是
的左右焦点分别是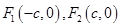 ,直线
,直线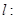
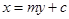 与椭圆
与椭圆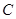 交于两点
交于两点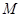 ,
,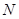 .当
.当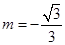 时,M恰为椭圆
时,M恰为椭圆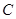 的上顶点,此时△
的上顶点,此时△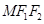 的周长为6.
的周长为6.
(Ⅰ)求椭圆
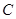 的方程;
的方程;(Ⅱ)设椭圆
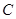 的左顶点为A,直线
的左顶点为A,直线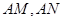 与直线
与直线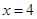 分别相交于点
分别相交于点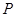 ,
,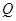 ,问当
,问当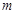
变化时,以线段
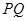 为直径的圆被
为直径的圆被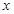 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值,若不是,说明理由.
(I)椭圆方程是: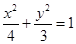 ;
;
(II)以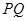 为直径的圆一定过右焦点
为直径的圆一定过右焦点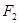 ,被
,被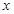 轴截得的弦长为定值6.
轴截得的弦长为定值6.
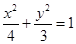 ;
;(II)以
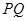 为直径的圆一定过右焦点
为直径的圆一定过右焦点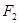 ,被
,被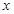 轴截得的弦长为定值6.
轴截得的弦长为定值6.本试题主要是考查了直线与椭圆的 位置关系的综合运用。
(1)由题意可知三角形的周长和斜率用参数a,b,c表示出来得到结论。
(2)当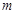 变化时,以线段
变化时,以线段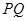 为直径的圆被
为直径的圆被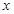 轴截得的弦长是否为定值,要分析m=0,m不为零的情况,结合直线与椭圆方程联立方程组,得到韦达定理和向量的关系来证明
轴截得的弦长是否为定值,要分析m=0,m不为零的情况,结合直线与椭圆方程联立方程组,得到韦达定理和向量的关系来证明
(1)由题意可知三角形的周长和斜率用参数a,b,c表示出来得到结论。
(2)当
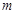 变化时,以线段
变化时,以线段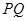 为直径的圆被
为直径的圆被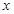 轴截得的弦长是否为定值,要分析m=0,m不为零的情况,结合直线与椭圆方程联立方程组,得到韦达定理和向量的关系来证明
轴截得的弦长是否为定值,要分析m=0,m不为零的情况,结合直线与椭圆方程联立方程组,得到韦达定理和向量的关系来证明
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
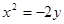 上有两点
上有两点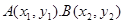 且
且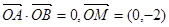 (0为坐标原点)
(0为坐标原点)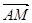 ∥
∥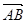 (2)若
(2)若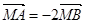 ,求AB所在直线方程。
,求AB所在直线方程。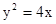 的焦点,与抛物线交与A、B两点,则
的焦点,与抛物线交与A、B两点,则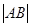 = .
= . 的离心率是
的离心率是



 ABC中,
ABC中, C=90°,AC="b," BC="a," P为三角形内的一点,且
C=90°,AC="b," BC="a," P为三角形内的一点,且 ,
,
 的双曲线与椭圆
的双曲线与椭圆 共焦点,则其渐近线方程是 .
共焦点,则其渐近线方程是 . 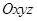 中,方程
中,方程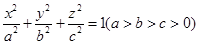 表示中心在原点、其轴与坐标轴重合的某椭球面的标准方程.
表示中心在原点、其轴与坐标轴重合的某椭球面的标准方程.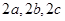 分别叫做椭球面的长轴长,中轴长,短轴长.类比在平面直角坐标系中椭圆标准方程的求法,在空间直角坐标系
分别叫做椭球面的长轴长,中轴长,短轴长.类比在平面直角坐标系中椭圆标准方程的求法,在空间直角坐标系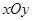 截椭球面所得椭圆的方程为
截椭球面所得椭圆的方程为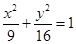 ,且过点M
,且过点M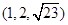 ,则此椭球面的标准方程为________
,则此椭球面的标准方程为________ 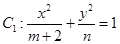 与双曲线
与双曲线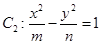 共焦点,则椭圆
共焦点,则椭圆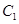 的离心率
的离心率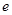 的取值范围为( )
的取值范围为( )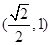

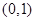

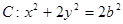 (常数
(常数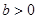 )的左右焦点分别为
)的左右焦点分别为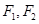 ,
,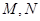 是直线
是直线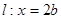 上的两个动点,
上的两个动点,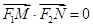 .
.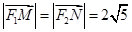 ,求
,求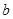 的值;
的值;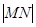 的最小值.
的最小值.