题目内容

2．如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别是棱BC，DD1上的点，如果B1E⊥平面ABF，则CE与DF的长度之和为（　　）
A．1B．$\frac{3}{2}$C．2$\sqrt{2}$D．$\sqrt{3}$

分析 利用B1E⊥平面ABF，可以证明△B1EB≌△BGC，所以CG=BE，从而可得CE与DF的长度之和为1．

解答 解：∵B1E⊥平面ABF，G在AB上．
∴B1E⊥BG，△B1EB≌△BGC，∴CG=BE，
∵CG=DF，BE+CE=1，
∴CE与DF的长度之和为1．
故选：A．

点评 本题以正方体为载体，考查线面位置关系，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
4．设区域Ω内的点（x，y）满足 $\left\{\begin{array}{l}{x^2+y^2+6x+6y+2＜0}\\{x^2-y^2+6x-6y＜0}\end{array}\right.$，则区域Ω的面积是8π；若x，y∈Z，则2x+y的最大值是-2．
5．已知不等式|x-a|＜b的解集为（-2，4），求a，b的值．
10．已知a，b∈R，函数f（x）=$\frac{1}{3}$x3+ax2+bx．
（1）若函数f（x）的图象过点P（1，$\frac{4}{3}$），且在点P处的切线斜率是3，求a，b的值；
（2）若x=-1是函数f（x）的极大值点，且x∈[-1，2]时，f（x）的最小值为-$\frac{2}{3}$，求a的值．
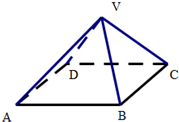17．如图：正四棱锥V-ABCD中，高为2，底面ABCD是边长为4的正方形，则二面角V-AB-C的平面角为45°．
7．已知函数f（x）=mx-lnx，（m＞0）．
（1）若m=1，求函数f（x）的极值；
（2）求函数f（x）在区间[1，e]上的最小值；
（3）若f（x）≤0恒成立，求m的取值范围．
14．已知函数f（x）=lnx-ax+1，x∈（0，+∞），a∈R）
（1）谈论函数f（x）在定义域内的极值点的个数
（2）设g（x）=mx-1（m＞0），在a=1时，求方程f（x）-g（x）=0的解的个数
（3）求证：（1+$\frac{3}{2×4}$）（1+$\frac{9}{4×10}$）（1+$\frac{27}{10×28}$）…[1+$\frac{{3}^{n}}{{{（3}^{n-1}+1）（3}^{n}+1）}$＜${e}^{\frac{3}{4}}$，（其中n∈N*，e是自然对数的底）
11．已知函数f（x）的导函数是f′（x）=3x2+2mx+9，f（x）在x=3处取得极值，且f（0）=0
（1）求f（x）的极大值和极小值
（2）设M（x，y）是曲线y=f（x）上的任意一点，当x∈（0，1]时，求直线OM斜率的最小值．
12．如图，一个靶子由四个同心圆组成，且半径分别为1，3，5，7，规定：击中A、B、C、D区域分别可获得5分、3分、2分、1分，脱靶（即击中最大圆之外的某点）得0分．甲射击时脱靶的概率为0.02，若未脱靶则等可能地击中靶子上的任意一点，求甲射击一次得分的数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网