题目内容
【题目】已知函数![]() ,
,![]() (
(![]() ,
,![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的极小值点;
的极小值点;
(2)当![]() 时,若
时,若![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)当![]() 时,
时,![]() ,则
,则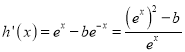 .
.
讨论![]() ,
,![]() 两种情况,研究单调性得极小值(2) (2)当
两种情况,研究单调性得极小值(2) (2)当![]() 时,
时,![]() 可化为
可化为![]() ,即
,即![]() ,令
,令![]() ,则
,则![]() .当
.当![]() 时,对于一切
时,对于一切![]() ,有
,有![]() ,
,![]() ,
,
所以![]() 恒成立.当
恒成立.当![]() 时,符合题意;当
时,符合题意;当![]() 时,存在
时,存在![]() ,使得
,使得![]() ,在
,在![]() 上
上![]() 单调递减,从而有:
单调递减,从而有:![]() 时,
时,![]() ,不符合题意,即得
,不符合题意,即得![]() 的取值范围
的取值范围
试题解析:
(1)当![]() 时,
时,![]() ,则
,则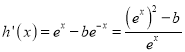 .
.
当![]() 时,
时,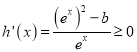 ,所以
,所以![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 无极值点;
无极值点;
当![]() 时,由
时,由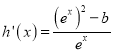
![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() 的极小值点为
的极小值点为![]() .
.
(2)当![]() 时,
时,![]() 可化为
可化为![]() ,即
,即![]() ,
,
令![]() ,则
,则![]() .
.
当![]() 时,对于一切
时,对于一切![]() ,有
,有![]() ,
,![]() ,
,
所以![]() 恒成立.
恒成立.
下面考虑![]() 时的情况.
时的情况.
当![]() 时,对于一切
时,对于一切![]() ,有
,有![]() ,
,![]() ,所以
,所以![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,符合题意;
,符合题意;
当![]() 时,
时,![]() ,
,![]() ,由零点存在性定理可知,一定存在
,由零点存在性定理可知,一定存在![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时,![]() ,所以在
,所以在![]() 上
上![]() 单调递减,从而有:
单调递减,从而有:![]() 时,
时,![]() ,不符合题意.
,不符合题意.
综上可知,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目