Question

【题目】已知数列满足，，，数列满足.

（1）证明是等差数列，并求的通项公式；

（2）设数列满足，，记表示不超过x的最大整数，求关于n的不等式的解集.

Answer 1

【答案】（1）证明见解析; （2）

【解析】

（1）根据等差数列定义,求得是常数即可证明为等差数列;由累加法,可求得数列的通项公式.

（2）由代入的通项公式中求得,同取倒数后可得,结合裂项法求和可得.判断出的单调性,即可求得的值域,即可求得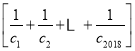的值.再解关于的不等式,即可求得正整数的值,即为不等式的解集.

（1）数列满足,数列满足

则

且,

所以数列是以为首项,公差为2的等差数列

则

即

利用递推公式可得

等式两边分别相加可得

而

所以

因为也满足上式

所以

（2）数列满足

则

同取倒数可得

即

所以

而

所以

由

可得

所以

所以

所以

则

所以由定义可得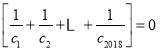

则不等式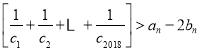等价于

而由（1）可知,,

所以

解得,又

所以

所以关于n的不等式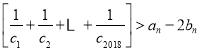的解集为