题目内容
如右图所示,已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2.
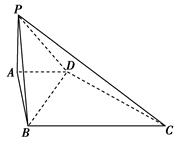
(1)求PC的长;
(2)求异面直线PC与BD所成角的余弦值的大小

(1)求PC的长;
(2)求异面直线PC与BD所成角的余弦值的大小
(1)因为PA⊥平面AC,AB⊥BC,∴PB⊥BC,即∠PBC=90°,由勾股定理得PB==.
∴PC==.
(2)
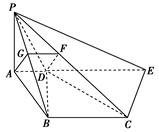
如右图所示,过点C作CE∥BD交AD的延长线于E,连结PE,则∠PCE为异面直线PC与BD所成的角或它的补角.
∵CE=BD=,且PE==.
∴由余弦定理得cos∠PCE==-.
∴PC与BD所成角的余弦值为.
∴PC==.
(2)

如右图所示,过点C作CE∥BD交AD的延长线于E,连结PE,则∠PCE为异面直线PC与BD所成的角或它的补角.
∵CE=BD=,且PE==.
∴由余弦定理得cos∠PCE==-.
∴PC与BD所成角的余弦值为.
略

练习册系列答案
相关题目
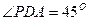 ,
, 求证:MN⊥平面PCD.
求证:MN⊥平面PCD.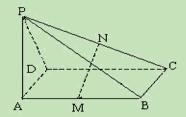
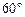 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
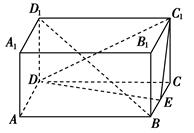
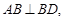 沿BD将
沿BD将 折起,使面
折起,使面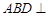 面
面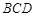 ,连结AC,则在四面体ABCD的四个面中,互相垂直的平面共有( )对
,连结AC,则在四面体ABCD的四个面中,互相垂直的平面共有( )对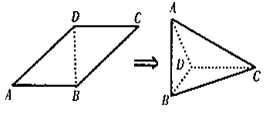
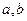 ,c和平面
,c和平面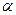 ,有以下六个命题:
,有以下六个命题: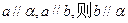 ②若
②若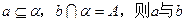 异面
异面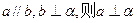 ④若
④若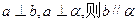
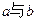 异面,
异面,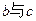 异面,则
异面,则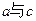 异面
异面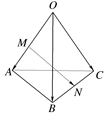
 b+c
b+c