题目内容
(本小题满分12分)如图,PA垂直于矩形 ABCD所在的平面,M、N分别是AB、PC的中点
⑴求证:MN∥平面PAD;
⑵若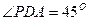 ,
, 求证:MN⊥平面PCD.
求证:MN⊥平面PCD.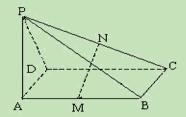
⑴求证:MN∥平面PAD;
⑵若
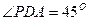 ,
, 求证:MN⊥平面PCD.
求证:MN⊥平面PCD.
解:⑴证明:取PD中点E,连结AE,EN,则有

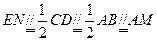
故AMNE是平行四边形
∴MN∥AE
又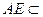 平面
平面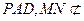 平面
平面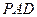
所以MN∥平面PAD ----------------------6分
⑵∵PA⊥平面ABCD,AD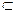 平面ABCD,
平面ABCD,
∴PA ⊥AD,又
⊥AD,又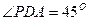
∴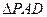 为等腰直角三角
为等腰直角三角 形
形
又E是PD中点
∴AE⊥PD,又AE∥MN
∴MN⊥PD
又ABCD为矩形
∴AB⊥AD
又AB⊥PA,AD∩P A=A
A=A
∴AB⊥平面PAD
∵AE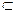 平面PAD-
平面PAD-
AB⊥AE 又AB∥CD,AE∥MN
又AB∥CD,AE∥MN
∴MN⊥CD
又∵PD∩CD=D
∴MN⊥平面PCD…………………………………12分

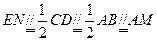
故AMNE是平行四边形
∴MN∥AE
又
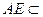 平面
平面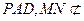 平面
平面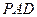
所以MN∥平面PAD ----------------------6分
⑵∵PA⊥平面ABCD,AD
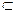 平面ABCD,
平面ABCD,∴PA
 ⊥AD,又
⊥AD,又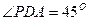
∴
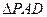 为等腰直角三角
为等腰直角三角 形
形又E是PD中点
∴AE⊥PD,又AE∥MN
∴MN⊥PD
又ABCD为矩形
∴AB⊥AD
又AB⊥PA,AD∩P
 A=A
A=A∴AB⊥平面PAD
∵AE
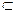 平面PAD-
平面PAD-AB⊥AE
 又AB∥CD,AE∥MN
又AB∥CD,AE∥MN∴MN⊥CD
又∵PD∩CD=D
∴MN⊥平面PCD…………………………………12分
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
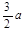
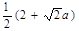
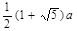
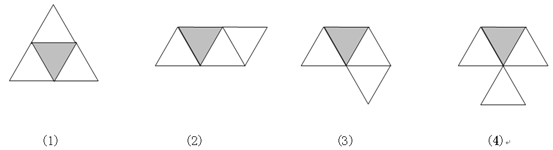
 (1)(3)
(1)(3)  (2)(4)
(2)(4)  (3)(4)
(3)(4)  (1)(2)
(1)(2)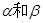 ,给定下列条件:
,给定下列条件: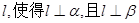 ;
; 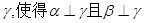 ;
;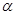 内有不共线的三点到
内有不共线的三点到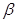 的距离相等;
的距离相等; 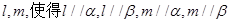
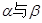 平行的条件有 ( )
平行的条件有 ( )

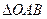 顶点
顶点 的坐标为
的坐标为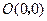 ,
,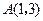 ,
,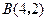 .
. 1)求点
1)求点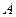 到直
到直 线
线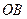 的距离
的距离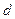 及
及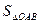 ;
;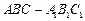 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成的角为
,侧棱与底面所成的角为 ,点
,点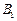 在底面上的射影
在底面上的射影 落在
落在 上.
上.
 ,求
,求 的值.
的值. ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小.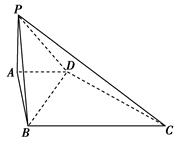
 的底面为矩形,
的底面为矩形, 且
且 平面
平面 分别为
分别为 的中点.
的中点.
 ;
; 的大小值.
的大小值.