题目内容
如右图所示,ABCD-A1B1C1D1是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点.
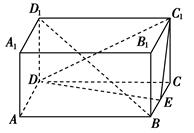
(1)求证:BD1∥平面C1DE;
(2)求三棱锥D-D1BC的体积.

(1)求证:BD1∥平面C1DE;
(2)求三棱锥D-D1BC的体积.
(1)证明:连接D1C交DC1于F,连结EF.
∵ABCD—A1B1C1D1为正四棱柱,
∴四边形DCC1D1为矩形,
∴F为D1C中点.
在△CD1B中,∵E为BC中点,∴EF∥D1B.
又∵D1B?面C1DE,EF?面C1DE,∴BD1∥平面C1DE.
(2)连结BD,VD-D1BC=VD1-DBC,∵AC′是正四棱柱,
∴D1D⊥面DBC.
∵DC=BC=2,∴S△BCD=×2×2=2.
VD1-DBC=·S△BCD·D1D=×2×1=.
∴三棱锥D-D1BC的体积为.
∵ABCD—A1B1C1D1为正四棱柱,
∴四边形DCC1D1为矩形,
∴F为D1C中点.
在△CD1B中,∵E为BC中点,∴EF∥D1B.
又∵D1B?面C1DE,EF?面C1DE,∴BD1∥平面C1DE.
(2)连结BD,VD-D1BC=VD1-DBC,∵AC′是正四棱柱,
∴D1D⊥面DBC.
∵DC=BC=2,∴S△BCD=×2×2=2.
VD1-DBC=·S△BCD·D1D=×2×1=.
∴三棱锥D-D1BC的体积为.
略

练习册系列答案
相关题目


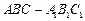 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成的角为
,侧棱与底面所成的角为 ,点
,点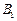 在底面上的射影
在底面上的射影 落在
落在 上.
上.
 ,求
,求 的值.
的值. ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小. 中.
中.
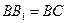 ,
,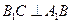 ,证明:平面
,证明:平面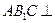 平面
平面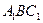 ;
;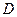 是
是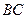 的中点,
的中点,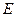 是
是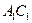 上的一点,
上的一点,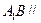 平面
平面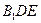 ,求
,求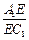 的值.
的值.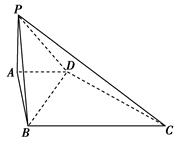

 的棱长均相等,则
的棱长均相等,则 与侧面
与侧面 所成角的正切值为 .
所成角的正切值为 .  ,若
,若 ,且
,且 与
与 相交但不垂直,直线
相交但不垂直,直线 分别为
分别为 ;②任意
;②任意 ; ③存在
; ③存在 ; ④存在
; ④存在 ; ⑤任意
; ⑤任意 ; ⑥存在
; ⑥存在 。真命题的序号是_________ 。
。真命题的序号是_________ 。