题目内容
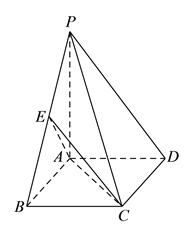
【题目】如图,多面体PABCD的直观图及三视图如图所示,E、F分别为PC、BD的中点.

(I)求证:EF∥平面PAD;
(II)求证:平面PDC⊥平面PAD.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(Ⅰ)由多面体PABCD的三视图知,四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是等腰三角形,PA=PD=![]() ,且平面PAD
,且平面PAD![]() 平面ABCD.先证明EF∥PA,由线面平行的判定定理证明EF∥平面PAD;
平面ABCD.先证明EF∥PA,由线面平行的判定定理证明EF∥平面PAD;
(Ⅱ)因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又CD⊥AD,所以,CD⊥平面PAD,∴CD⊥PA又可得△PAD是等腰直角三角形,所以PA⊥AD,根据线面垂直的判定定理得PA⊥平面PDC,又PA平面PAD,所以平面PAD⊥平面PDC.
试题解析:
(I)证明:由多面体![]() 的三视图知,四棱锥
的三视图知,四棱锥![]() 的底面
的底面![]() 是边长为
是边长为![]() 的正方形,侧面
的正方形,侧面![]() 是等腰三角形,
是等腰三角形,![]() ,且平面
,且平面![]() 平面
平面![]() . 连结
. 连结![]() ,则
,则![]() 是
是![]() 的中点,在△
的中点,在△![]() 中,
中,![]() ,且
,且![]()
平面![]() ,
,![]()
平面![]() ,
,
∴![]() ∥平面
∥平面![]()
(2) 因为平面![]() ⊥平面
⊥平面![]() , 平面
, 平面![]() ∩平面
∩平面![]() , 又
, 又![]() ⊥
⊥![]() ,所以,
,所以,![]() ⊥平面
⊥平面![]() ,∴
,∴![]() ⊥
⊥![]() 又
又![]() ,
,![]() ,所以△
,所以△![]() 是
是
等腰直角三角形,且![]() ,即
,即![]() 又CD∩PD=D, ∴PA⊥平面PDC,又PA平面PAD,所以平面PAD⊥平面PDC.
又CD∩PD=D, ∴PA⊥平面PDC,又PA平面PAD,所以平面PAD⊥平面PDC.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目