题目内容
【题目】已知点E（﹣2，0），点P时圆F：（x﹣2）2+y2=36上任意一点，线段EP的垂直平分线交FP于点M，点M的轨迹记为曲线C．
（Ⅰ）求曲线C的方程；
（Ⅱ）过F的直线交曲线C于不同的A、B两点，交y轴于点N，已知 
=m 
， 
=n 
，求m+n的值．
【答案】解：（Ⅰ）由题意知，|ME|+|MF|=|MP|+|MF|=r=6＞|EF|=4，
故由椭圆定义知，点M的轨迹是以点E，F为焦点，长轴为6，焦距为4的椭圆，从而长半轴长为a=3，短半轴长为b= 
= 
，
∴曲线C的方程为： 
（Ⅱ）由题知F（2，0），
若直线AB恰好过原点，则A（﹣3，0），B（3，0），N（0，0），
∴ 
=（﹣3，0）， 
=（5，0），则m= 
，
=（3，0）， 
=（﹣1，0），则n=﹣3，
∴m+n= 
．
若直线AB不过原点，设直线AB：x=ty+2，t≠0，
A（ty1+2，y1），B（ty2+2，y2），N（0，﹣ 
）．
则 =（ty1+2，y1+ ）， =（﹣ty1，﹣y1），
=（ty2+2，y2+ ）， =（﹣ty2，﹣y2），
由 
，得y1+ =m（﹣y1），从而m= 
；
由 
，得y2+ =n（﹣y2），从而n= 
；
故m+n= +（ ）= 
=﹣2﹣ 
．
联立方程组得：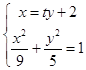 
，整理得（5t2+9）y2+20ty﹣25=0，
∴y1+y2=﹣ 
，y1y2= 
，
∴m+n=﹣2﹣ ═ 
=﹣2﹣ 
= ．
综上所述，m+n=
【解析】（Ⅰ）求出|ME|+|MF|=6＞|EF|=4，判断点M的轨迹是以点E，F为焦点，长轴为6，焦距为4的椭圆，
然后求解方程．（Ⅱ）求出F（2，0），若直线AB恰好过原点，计算m+n的值即可；若直线AB不过原点，设直线AB：x=ty+2，t≠0，求出相关点的坐标与向量，表示出+n，联立直线与椭圆方程的方程组，利用韦达定理，转化求解即可．
