题目内容
已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=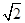 ,O为AB的中点.
,O为AB的中点.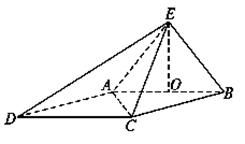
(Ⅰ)求证:EO⊥平面ABCD;
(Ⅱ)求点D到平面AEC的距离.
(Ⅰ)详见解析; (Ⅱ) 点D到平面AEC的距离为 .
.
解析试题分析:(Ⅰ)求证EO⊥平面ABCD,只需证明 垂直平面
垂直平面 内的两条直线即可,注意到
内的两条直线即可,注意到 ,则
,则 为等腰直角三角形,
为等腰直角三角形, 是
是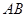 的中点,从而得
的中点,从而得 ,由已知可知
,由已知可知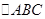 为边长为2的等边三角形,可连接CO,利用勾股定理,证明EO⊥CO,利用线面垂直的判定,可得EO⊥平面ABCD;(Ⅱ)求点D到平面AEC的距离,求点到平面的距离方法有两种,一.垂面法,二.等体积法,此题的体积容易求,且
为边长为2的等边三角形,可连接CO,利用勾股定理,证明EO⊥CO,利用线面垂直的判定,可得EO⊥平面ABCD;(Ⅱ)求点D到平面AEC的距离,求点到平面的距离方法有两种,一.垂面法,二.等体积法,此题的体积容易求,且 的面积也不难求出,因此可利用等体积,即
的面积也不难求出,因此可利用等体积,即 ,从而可求点D到面AEC的距离.
,从而可求点D到面AEC的距离.
试题解析:(Ⅰ)连接CO.
∵ ,∴△AEB为等腰直角三角形. 1分
,∴△AEB为等腰直角三角形. 1分
∵O为AB的中点,∴EO⊥AB,EO=1. 2分
又∵四边形ABCD是菱形,∠ABC=60°,
∴△ACB是等边三角形,
∴CO=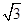 . 3分
. 3分
又EC=2,∴EC2=EO2+CO2,∴EO⊥CO. 4分
又CO?平面ABCD,EO 平面ABCD,∴EO⊥平面ABCD. 6分
平面ABCD,∴EO⊥平面ABCD. 6分
(Ⅱ)设点D到平面AEC的距离为h.
∵AE=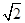 ,AC=EC=2,∴S△AEC=
,AC=EC=2,∴S△AEC= . 8分
. 8分
∵S△ADC=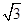 ,E到平面ACB的距离EO=1,VD-AEC=VE-ADC, 9分
,E到平面ACB的距离EO=1,VD-AEC=VE-ADC, 9分
∴S△AEC·h=S△ADC·EO,∴h= , 11分
, 11分
∴点D到平面AEC的距离为 . 12分
. 12分
考点:线线垂直的判定、线面垂直的判定,以及棱锥的体积公式,点到平面距离.

 中,底面
中,底面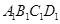 是正方形,
是正方形, 是
是 的中点,
的中点,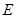 是棱
是棱 上任意一点.
上任意一点.
 ;
; ,求
,求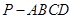 中,底面
中,底面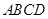 为菱形,
为菱形,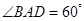 ,
, 为
为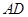 的中点.
的中点.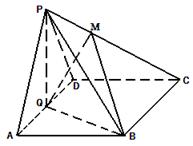
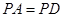 ,求证:平面
,求证:平面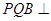 平面
平面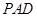 ;
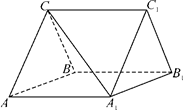
;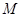 在线段
在线段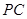 上,
上,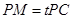 ,试确定
,试确定 的值,使
的值,使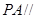 平面
平面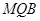 .
.
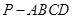 中,底面
中,底面 是边长为
是边长为 的正方形,侧面
的正方形,侧面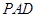
 底面
底面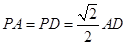 ,设
,设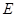 、
、 分别为
分别为 、
、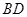 的中点.
的中点.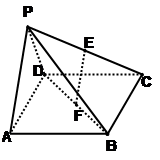
 //平面
//平面
 .
.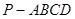 中,底面
中,底面 是个边长为
是个边长为 的正方形,侧棱
的正方形,侧棱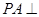 底面
底面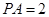 ,
,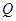 是
是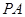 的中点.
的中点.
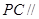 平面
平面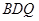 ;
; 的体积.
的体积.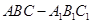 中, D是 AC的中点。
中, D是 AC的中点。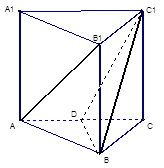
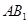 //平面
//平面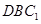
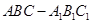 中,
中,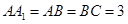 ,
,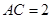 ,
, 是
是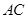 的中点.
的中点.
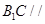 平面
平面 ;
;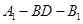 的余弦值.
的余弦值.