题目内容
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.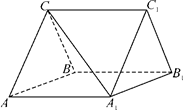
(Ⅰ)证明:AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
(I)见解析;(II) .
.
解析试题分析:(I)取 得中点
得中点 ,连接
,连接 ,
, ,
, ,由此可证
,由此可证 ,
, 平面
平面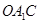 ,进而可得
,进而可得 ;(II)易证
;(II)易证 ,
, ,
, 两两垂直,以
两两垂直,以 坐标原点,
坐标原点, 的方向为
的方向为 轴的正向,建立空间直角坐标系,可得
轴的正向,建立空间直角坐标系,可得 ,
, ,
, 的坐标,设
的坐标,设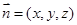 是平面
是平面 的一法向量,求出法向量
的一法向量,求出法向量 ,继而求得
,继而求得 ,即为所求角的正弦值.
,即为所求角的正弦值.
试题解析:(I)取 得中点
得中点 ,连接
,连接 ,
, ,
,
因为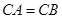 ,所以
,所以 ,由于
,由于 ,
,
所以 为等边三角形,所以
为等边三角形,所以 ,
,
又因为 ,所以
,所以 平面
平面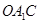 ,
,
又 平面
平面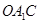 ,故
,故 ;
;
(II)由(Ⅰ)知 ,
,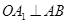 ,
,
又∵面 面
面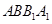 ,面
,面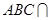 面
面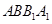
 ,∴
,∴ 面
面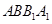 ,∴
,∴
 ,
,
∴ ,
,
 两两相互垂直,以
两两相互垂直,以 为坐标原点,
为坐标原点, 的方向为
的方向为 轴正方向,|
轴正方向,| |为单位长度,建立如图所示空间直角坐标系
|为单位长度,建立如图所示空间直角坐标系 ,设
,设

有题设知 (1,0,0),
(1,0,0), (0,
(0,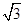 ,0),
,0),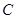 (0,0,
(0,0,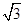 ),
),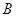 (-1,0,0),则
(-1,0,0),则 =(1,0,
=(1,0,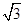 ),
), =
=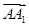 =(-1,0,
=(-1,0,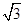 ),
), =(0,-
=(0,-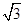 ,
,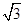 ),
),
设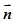 =
= 是平面
是平面 的法向量,
的法向量,
则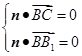 ,即
,即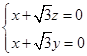 ,可取
,可取

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
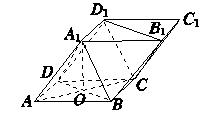
 底面ABCD,PD
底面ABCD,PD ADC-900,AB=AD=PD=1.CD=2.
ADC-900,AB=AD=PD=1.CD=2.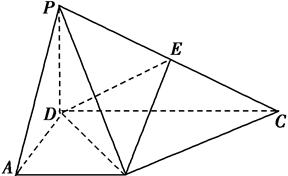
 ,试确定
,试确定 的值,使得二面角
的值,使得二面角 .
.
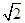 .
.
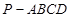 的底面是正方形,
的底面是正方形,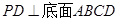 ,点
,点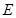 在棱
在棱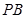 上.
上.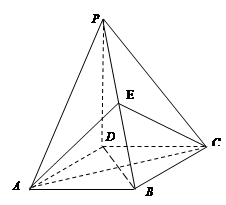
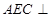 平面
平面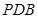 ;
;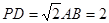 ,且
,且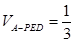 时,确定点
时,确定点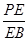 的值.
的值.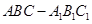 中,
中,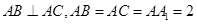 ,点
,点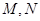 分别为
分别为 和
和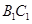 的中点.
的中点.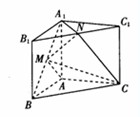
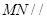 平面
平面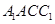 ;
;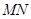 和
和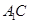 所成的角.
所成的角.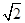 ,O为AB的中点.
,O为AB的中点.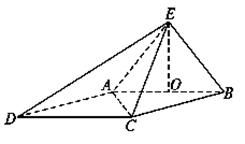
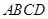 中,
中,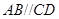 ,
,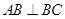 ,
,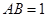 ,
,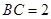 ,
,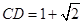 ,过
,过 作
作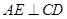 ,垂足为
,垂足为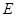 .
.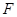 、
、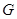 分别是
分别是 、
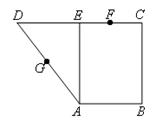
、 的中点.现将
的中点.现将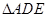 沿
沿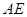 折起,使二面角
折起,使二面角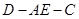 的平面角为
的平面角为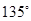 .
.

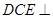 平面
平面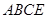 ;
;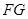 与面
与面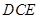 所成角的正弦值.
所成角的正弦值.
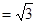 ,求证:平面ADE⊥平面PBC
,求证:平面ADE⊥平面PBC