题目内容
2．若函数f（x）=x（x-c）2在x=1处有极小值，则常数c的值为1．分析 求导数可得f′（x）=（x-c）（3x-c），令其为0，分类讨论可得函数取极小值的情形，比较已知可得c的方程，解之可得．
解答 解：展开可得f（x）=x（x-c）2=x3-2cx2+c2x，
求导数可得f′（x）=3x2-4cx+c2=（x-c）（3x-c）
令f′（x）=（x-c）（3x-c）=0可得x=c，或x=$\frac{c}{3}$，
当c=0时，函数无极值，不合题意，
当c＞0时，可得函数在（-∞，$\frac{c}{3}$）单调递增，在（$\frac{c}{3}$，c）单调递减，在（c，+∞）单调递增，
故函数在x=c处取到极小值，故c=1，符合题意；
当c＜0时，可得函数在（-∞，c）单调递增，在（c，$\frac{c}{3}$）单调递减，在（$\frac{c}{3}$，+∞）单调递增，
故函数在x=$\frac{c}{3}$处取到极小值，故c=3，矛盾，
故答案为：1．
点评 本题考查利用导数研究函数的极值，涉及分类讨论的思想，属中档题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
13．如图的框图表示的算法的功能是（ ）
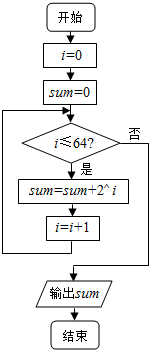
| A． | 求和S=2+22+…+264 | B． | 求和S=1+2+22+…+263 | ||
| C． | 求和S=1+2+22+…+264 | D． | 以上均不对 |
10．命题“?x0∈R，2${\;}^{{x}_{0}}$≥1”的否定是（ ）
| A． | ?x0∈R，2${\;}^{{x}_{0}}$＜1 | B． | ?x0∈R，2${\;}^{{x}_{0}}$≤1 | C． | ?x∈R，2x≥1 | D． | ?x∈R，x＜1 |
17．函数f（x）=2x-sinx在（-∞，+∞）上（ ）
| A． | 是增函数 | B． | 是减函数 | C． | 有最大值 | D． | 有最小值 |
11．某校高一年段为了控制学生迟到现象，特别规定在每周周一到周五这五天中，“连续5天，每天迟到都不超过5人次的班级才有资格争夺年段流动红旗”．根据过去5天年段统计的一到四班迟到学生人此数据的数字特征，一定有资格的是（ ）
| A． | 一班：总体均值为2，总体方差为2 | B． | 二班：总体均值为3，中位数为3 | ||
| C． | 三班：总体均值为2，总体方差大于0 | D． | 四班：中位数为2，众数为2 |