题目内容
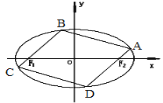
【题目】已知点![]() 在椭圆G:
在椭圆G:![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() .
.
![]() 求椭圆G的方程;
求椭圆G的方程;
![]() 若斜率为1的直线l与椭圆G交于A、B两点,以AB为底做等腰三角形,顶点为
若斜率为1的直线l与椭圆G交于A、B两点,以AB为底做等腰三角形,顶点为![]() ,求
,求![]() 的面积.
的面积.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题(Ⅰ) 由条件可得方程组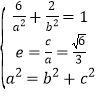 ,解得
,解得![]() ,
,![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() . (Ⅱ)直线与椭圆弦长、面积问题,一般利用直线方程与椭圆方程联立方程组,转化为一元二次方程,利用韦达定理、点到直线距离公式、弦长公式解决:本题关键转化以
. (Ⅱ)直线与椭圆弦长、面积问题,一般利用直线方程与椭圆方程联立方程组,转化为一元二次方程,利用韦达定理、点到直线距离公式、弦长公式解决:本题关键转化以![]() 为底作等腰三角形,顶点为
为底作等腰三角形,顶点为![]() 为
为![]() ,其中
,其中![]() 中点为
中点为![]() ,这样可得等量关系
,这样可得等量关系![]() ,利用韦达定理可得弦中点坐标:
,利用韦达定理可得弦中点坐标:![]() ,解得
,解得![]() ,进而可得
,进而可得![]() 、
、![]() 两点坐标,以下就具体化了.
两点坐标,以下就具体化了.
试题解析:解:(1)由题意可得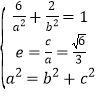 ,解得
,解得![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() ……(*)
……(*)
设![]() ,
,![]()
![]() ,
,![]() 中点为
中点为![]() ,
,
则![]() ,
,![]() ,
,
因为![]() 为等腰
为等腰![]() 的底边,所以
的底边,所以![]() ,
,
所以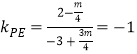 ,解得
,解得![]() ,所以方程(*)为
,所以方程(*)为![]() ,
,
解得![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,于是
,于是![]() ,
,
此时,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以△![]() 的面积为
的面积为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目