题目内容
设数列{an}(n∈N*)是等差数列,Sn是其前n项和,d为公差,且S2010<S2011,S2011=S2012,给出下列五个结论,正确的个数为( )
①d<0;
②a2012=0;
③a2011=-a2013;
④S2010=S2013;
⑤S2011与S2012均为Sn的最大值.
①d<0;
②a2012=0;
③a2011=-a2013;
④S2010=S2013;
⑤S2011与S2012均为Sn的最大值.
| A.2个 | B.3个 | C.4个 | D.5个 |
∵数列{an}(n∈N*)是等差数列,Sn是其前n项和,d为公差,
S2010<S2011,S2011=S2012,
∴a2011=S2011-S2010>0,
a2012=S2012-S2011=0,
∴d=a2012-a2011<0,
故①和②都正确;
∵a2011=a2012-d=0-d=-d,
a2013-a2012=a2013=d,
∴a2011=-a2013,即③正确;
∵a2011=-a2013,
∴S2010=S2013,即④正确;
∵d<0,a2012=0,
∴S2011与S2012均为Sn的最大值,即⑤正确.
故选D.
S2010<S2011,S2011=S2012,
∴a2011=S2011-S2010>0,
a2012=S2012-S2011=0,
∴d=a2012-a2011<0,
故①和②都正确;
∵a2011=a2012-d=0-d=-d,
a2013-a2012=a2013=d,
∴a2011=-a2013,即③正确;
∵a2011=-a2013,
∴S2010=S2013,即④正确;
∵d<0,a2012=0,
∴S2011与S2012均为Sn的最大值,即⑤正确.
故选D.

练习册系列答案
相关题目
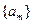 的前
的前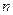 项和为
项和为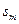 .若
.若 .
.