题目内容
【题目】在等差数列![]() 中,已知
中,已知![]() .在①
.在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个补充在第(2)问中,并对其求解.
这三个条件中任选一个补充在第(2)问中,并对其求解.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)若___________,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】
本题第(1)题先设等差数列![]() 的公差为
的公差为![]() ,然后根据已知条件列出关于首项
,然后根据已知条件列出关于首项![]() 与公差
与公差![]() 的方程组,解出
的方程组,解出![]() 与
与![]() 的值,即可得到等差数列
的值,即可得到等差数列![]() 的通项公式;
的通项公式;
第(2)题对于方案一:选条件①,先根据第(1)题的结果计算出数列![]() 的通项公式,然后运用裂项相消法可计算出前
的通项公式,然后运用裂项相消法可计算出前![]() 项和
项和![]() ;对于方案二:选条件②,先根据第(1)题的结果计算出数列
;对于方案二:选条件②,先根据第(1)题的结果计算出数列![]() 的通项公式,然后分
的通项公式,然后分![]() 为偶数和奇数两种情况分别求和,并运用分组求和法和等差数列的求和公式进行计算,即可计算出前
为偶数和奇数两种情况分别求和,并运用分组求和法和等差数列的求和公式进行计算,即可计算出前![]() 项和
项和![]() ;对于方案三:选条件③,先根据第(1)题的结果计算出数列
;对于方案三:选条件③,先根据第(1)题的结果计算出数列![]() 的通项公式,然后根据通项公式的特点运用错位相减法可计算出前
的通项公式,然后根据通项公式的特点运用错位相减法可计算出前![]() 项和
项和![]() .
.
解:(1)设等差数列![]() 的公差为
的公差为![]() ,则
,则![]() ,
,
即![]() ,
,
故![]()
![]() .
.
(2)选①,
由![]()
![]() 得
得![]() .
.
选②,由![]() 得
得
当![]() 为偶数时,
为偶数时,![]()
![]() .
.
当![]() 为奇数时,
为奇数时,![]()
![]() ,
,
故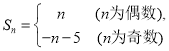
选③,
由![]() 得
得
![]() ,①
,①
则![]() ,②
,②
①-②,得
![]()
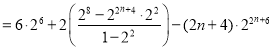
![]() ,
,
故.![]()

【题目】“支付宝捐步”已经成为当下最热门的健身方式,为了了解是否使用支付宝捐步与年龄有关,研究人员随机抽取了5000名使用支付宝的人员进行调查,所得情况如下表所示:
50岁以上 | 50岁以下 | |
使用支付宝捐步 | 1000 | 1000 |
不使用支付宝捐步 | 2500 | 500 |
(1)由上表数据,能否有99.9%的把握认为是否使用支付宝捐步与年龄有关?
(2)55岁的老王在了解了捐步功能以后开启了自己的捐步计划,可知其在捐步的前5天,捐步的步数与天数呈线性相关.
第x天 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
步数 | 4000 | 4200 | 4300 | 5000 | 5500 |
(i)根据上表数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(ii)记由(i)中回归方程得到的预测步数为![]() ,若从5天中任取3天,记
,若从5天中任取3天,记![]() 的天数为X,求X的分布列以及数学期望.
的天数为X,求X的分布列以及数学期望.
附参考公式与数据: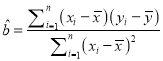 ,
,![]() ;K2=
;K2=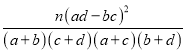 ;
;
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |